Кусочно-линейная функция Задачи с решениями
Задачи с решениями

Докажите, что функция y = |x + 4| – |x – 1| + |x – 3| – 2x – 3 убывает на всей числовой оси.
Решение
Эта функция – ломаная с вершинами в точках с абсциссами, равными –4, 1, 3. На каждом из звеньев график ломаной задается уравнением какой-либо прямой.
При x ≤ –4 выражения в каждом из модулей меньше нуля, y = –3x – 5. При
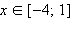 y = –x + 3, при
y = –x + 3, при
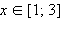 y = –3x + 5, при x ≥ 3, y = –x – 1. Таким образом, на каждом из участков угловой коэффициент прямой, содержащей соответствующее звено, отрицательный. Таким образом, функция убывает на каждом из звеньев ломаной. Из непрерывности функции можно сделать вывод, что она убывает и на всей области определения.
y = –3x + 5, при x ≥ 3, y = –x – 1. Таким образом, на каждом из участков угловой коэффициент прямой, содержащей соответствующее звено, отрицательный. Таким образом, функция убывает на каждом из звеньев ломаной. Из непрерывности функции можно сделать вывод, что она убывает и на всей области определения.
 2 из 2
2 из 2
 |


 Задачи с решениями
Задачи с решениями

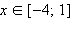
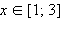
 2 из 2
2 из 2
