Решение.
Пусть y = cos x. Тогда задача сводится к поиску наибольшего значения функции 2y2 – 5y + 1 на отрезке [–1; 1]. Это квадратичная функция, и вершина параболы
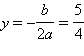лежит вне отрезка [–1; 1] справа от него. Таким образом, на отрезке [–1; 1] функция f убывает, и ее наибольшее значение достигается в точке f (–1) = 8.
Задачи
8 из 8
