Решение.
По обратной теореме Виета решениями уравнения, соответствующего первому неравенству, являются числа –2 и a2 + b2, решениями уравнения, соответствующего второму неравенству, – числа 25/4 и –(a + b). Решениями первого неравенства являются все числа из интервала (–2; a2 + b2). Решениями второго неравенства являются все числа, лежащие вне интервала с концами в точках 25/4 и –(a + b).
Система неравенств не имеет решений только тогда, когда интервал, соответствующий первому неравенству, целиком содержится внутри интервала, соответствующего второму неравенству. Одно из чисел 25/4 и –(a + b) должно быть не меньше, чем a2 + b2, а второе – не больше, чем –2. Т.к. 25/4 > –2, то
Фигура Ф, задаваемая приведенной системой неравенств, – это сегмент, ограниченный дугой окружности радиуса 5/2 с центром в начале координат, и полуплоскостью a + b ≥ 3. Ее площадь S = S1 – S2, где S1 – площадь сектора AOB, S2 – площадь треугольника AOB.
Координаты точек A и B находятся из системы уравнений
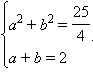 Решив ее, получим
Решив ее, получим
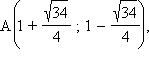
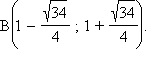 Отсюда
Отсюда
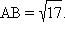
Пусть C – середина AB. Тогда
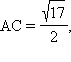
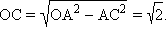 Площадь сектора
Площадь сектора
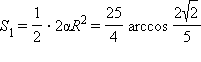 (здесь α –
(здесь α –
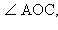
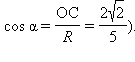 Площадь треугольника
Площадь треугольника
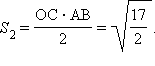 Площадь фигуры Ф, таким образом, составляет
Площадь фигуры Ф, таким образом, составляет
function showUserAnswer(){
testSolution='

 Задачи
Задачи

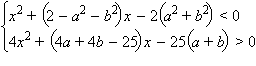
 1 из 5
1 из 5
