Задачи с решениями

На координатной плоскости рассматривается фигура Ф, состоящая из всех точек, координаты которых (a; b) таковы, что система уравнений 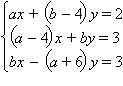имеет единственное решение. Изобразите фигуру Ф и составьте уравнения всех прямых, каждая из которых проходит через точку B (0; 7) и имеет с фигурой Ф единственную общую точку.

Решим систему относительно x и y. Исключая из уравнений по очереди x и y, получим:

• Пусть a + b ≠ 4. Тогда система имеет единственное решение
  
   
  Подставляя эти значения в третье уравнение исходной системы, получим уравнение окружности 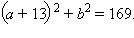Для всех (a; b), за исключением тех, для которых a + b = 4, система имеет единственное решение. Решив совместно уравнения 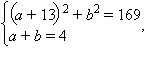найдем, что исключениями являются точки (–1; 5) и (8; 12).
• Пусть a + b = 4. Тогда исходная система равносильна системе
  
  
  Из первых двух уравнений следует, что a = –8 (при этом b = 12). В этом случае наша система равносильна системе
  
  
  имеющей единственное решение.

Итак, фигура Ф – окружность, определяемая уравнением (a + 13)² + b² = 169, с выколотой точкой A (–1; 5).

Из всех прямых, проходящих через точку B, единственную общую точку с этой фигурой имеют три прямые. Одна из них проходит через выколотую точку A: это прямая 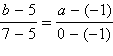или b = 2a + 7. Две другие касаются окружности; чтобы их найти нужно подставить уравнение прямой, проходящей через точку B (это уравнение: b = ka + 1 – k) в уравнение окружности, и найти, при каких k оно имеет единственное решение. Приравнивая дискриминант квадратного уравнения к нулю, получаем a = 0 и

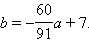
Таким образом, искомыми прямыми являются прямые b = 2a + 7, a = 0,

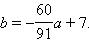
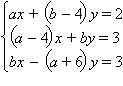
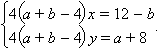
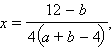
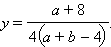
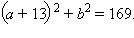
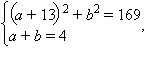
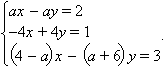
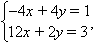
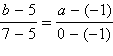
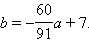
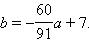
5 из 5