Экстремумы Задачи с решениями
Задачи с решениями

Среди всевозможных парабол с вершиной в точке с абсциссой x = –1 и касающихся прямой y = 2x + 1, найдите ту, которая пересекает ось OY с наименьшей по модулю ординатой.
Решение
Парабола симметрична оси x = –1, поэтому ее уравнение можно записать в виде
y = a (x + 1)2 + b.
Она касается прямой y = 2x + 1, если уравнение
a (x + 1)2 + b = 2x + 1
имеет единственный корень, что, в свою очередь, возможно, если дискриминант этого квадратного уравнения равен нулю, т.е.
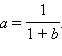 Итак, уравнение параболы нужно искать в виде
Итак, уравнение параболы нужно искать в виде
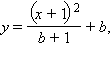 где b – некоторая постоянная. Определить ее нам поможет последнее условие: ордината пересечения с осью OY должна быть наименьшей, т.е.
где b – некоторая постоянная. Определить ее нам поможет последнее условие: ордината пересечения с осью OY должна быть наименьшей, т.е.
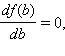 где
где
Получаем
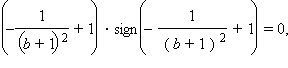 откуда находим точки, подозрительные на экстремум,
откуда находим точки, подозрительные на экстремум,
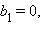
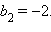 Исследуя знаки производной на отрезках (–∞; –2), (–2; –1), (–1; 0), (0; +∞), получим, что функция достигает минимума в точке b = –2.
Таким образом, парабола имеет уравнение
Исследуя знаки производной на отрезках (–∞; –2), (–2; –1), (–1; 0), (0; +∞), получим, что функция достигает минимума в точке b = –2.
Таким образом, парабола имеет уравнение
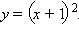
 4 из 4
4 из 4
 |


 Задачи с решениями
Задачи с решениями

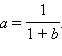
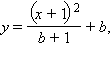
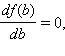
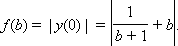
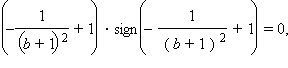
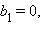
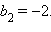
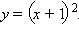
 4 из 4
4 из 4
