Дифференциальные уравнения первого порядка
Задачи с решениями
Решите уравнение
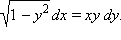
Решение
Данное уравнение является дифференциальным уравнением с разделяющимися переменными. Перенесем все множители с x в левую часть, а с y – в правую:
Проинтегрируем обе части уравнения:
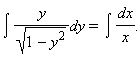Интеграл от правой части равен ln x + C2. Интеграл от левой части берется подстановкой y = sin z:
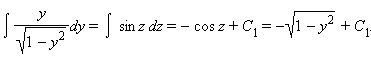Отсюда
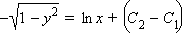или
При делении на x мы допустили неравносильный переход; проверкой убеждаемся, что x = 0 также является решением (особым) нашего уравнения.
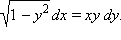
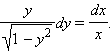
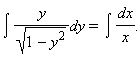
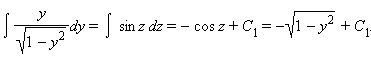
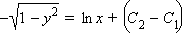
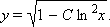
1 из 6
 |
