Дифференциальные уравнения первого порядка
Задачи с решениями
Решите уравнение
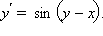
Решение
Пусть z = y – x. Тогда dz = dy – dx или
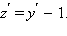Получаем
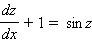и
Чтобы взять интеграл в левой части уравнения, воспользуемся универсальной подстановкой
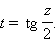Тогда
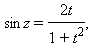
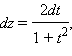и получаем
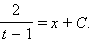Возвращаясь к исходным переменным, получим
Особым решением уравнения является функция
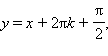
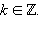
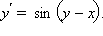
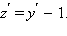
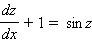
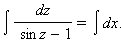
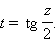
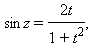
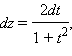
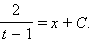
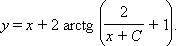
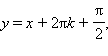
3 из 6
 |
