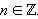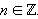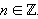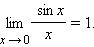Справочник

R.1. Основные формулы

R.1.3. Тригонометрические функции

Длина дуги, содержащей центральный угол x:

l = Rx.

Площадь сектора, содержащего центральный угол x:

Площадь круга:

S = πR2.

Тангенс и котангенс:

sin2 x + cos2 x = 1.

Формулы приведения:

cos (x + π) = –cos x,	cos (π – x) = –cos x,
sin (x + π) = –sin x,	sin (π – x) = sin x,
tg (π – x) = –tg x,	ctg (π – x) = –ctg x,

Формулы сложения и вычитания аргументов тригонометрических функций:

sin (x + y) = sin x cos y + cos x sin y,

sin (x – y) = sin x cos y – cos x sin y,

cos (x + y) = cos x cos y – sin x sin y,

cos (x – y) = cos x cos y + sin x sin y,

tg (x + y) =	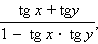tg (x – y) =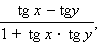
ctg (x + y) =	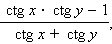ctg (x – y) =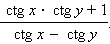

Формулы двойных аргументов:

sin 2x = 2sin x cos x,	cos 2x = cos2x – sin2x = 2cos2x – 1 = 1 – 2sin2x,
tg 2x =	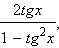ctg 2x =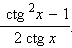

Формулы половинного аргумента:

Формулы преобразования суммы и разности тригонометрических функций в произведение:

Решения уравнения sin x = a :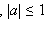

x = (–1)n arcsin a + πn,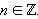

Решения уравнения cos x = a :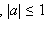

x = ±arccos a + 2πn,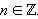

Решения уравнения tg x = a:

x = arctg a + πn,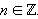

Решения уравнения сtg x = a:

x = arcсtg a + πn,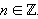

Первый замечательный предел:
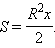
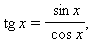
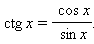
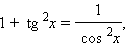
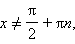
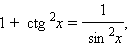
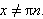
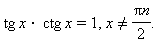
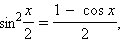
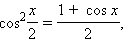
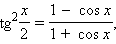
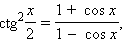
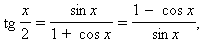
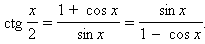
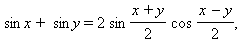
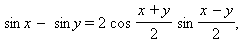
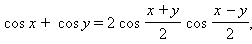
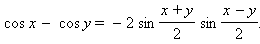
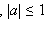
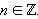
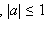