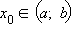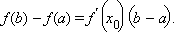Глава 3. Дифференцирование и интегрирование функций

Модель 3.6.  Теорема Лагранжа

Согласно теореме Лагранжа, если функция f (x) непрерывна на отрезке [a; b] и дифференцируема на интервале (a; b), то существует хотя бы одна точка 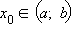такая, что

В левой части модели показан график функции y (x) = 0,4x³ – 5,3x² + 19,8x – 18,9. Функцию можно изменить, перетаскивая любую из четырех выделенных точек при помощи мыши. Задайте границы отрезка при помощи полей численного ввода в верхнем правом углу модели (либо передвигая точки на графике функции) и нажмите кнопку Старт. Красным будет выделена хорда, соединяющая точки a и b, серым – искомая касательная. В окне вывода появится абсцисса точки касания.

Управление анимацией производится кнопками Стоп и Сброс.