Глава 3. Дифференцирование и интегрирование функций

Модель 3.5.
Линеаризация функций
Интерактивная модель демонстрирует линеаризацию функций в точке x0 при помощи рядов Тейлора.
Линеаризация функций применяется для нахождения пределов в точке, при построении графиков функций, для решения уравнений. Суть метода состоит в том, что в окрестности какой-либо точки, в которой функция f (x) непрерывна и дифференцируема нужное количество раз, ее можно заменить ее касательной f (x0) + f' (x0) · (x – x0). Чем ближе к x0 находится точка x, тем больше точность данного приближения.
Для более точного исследования поведения функции в окрестности некоторой точки применяется разложение в степенной ряд 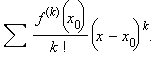 Если оставить в разложении нулевой и первый члены ряда, то мы получим приближение функции в окрестности некоторой точки ее касательной в этой точке.
Если оставить в разложении нулевой и первый члены ряда, то мы получим приближение функции в окрестности некоторой точки ее касательной в этой точке.
Введите в поле ввода в правом верхнем углу модели функцию f (x) и нажмите Enter. Установите при помощи поля численного ввода абсциссу точки, в которой производится разложение в ряд Тейлора (эта точка должна входить в область определения функции). Сама функция будет построена на экране черной линией. Цветными линиями (значение каждой из них указано в легенде) обозначаются отдельные члены степенного ряда, а также сумма членов ряда с первого до данного включительно. Включить или отключить отображение графика того или иного члена ряда можно при помощи двух столбцов выключателей, а также при помощи двух пар кнопок под этими столбцами, первые из которых включают графики всех членов ряда (до восьмого включительно), а вторые – отключают.



 Модель 3.5.
Линеаризация функций
Модель 3.5.
Линеаризация функций Модель 3.5.
Линеаризация функций
Модель 3.5.
Линеаризация функций
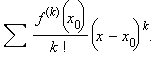 Если оставить в разложении нулевой и первый члены ряда, то мы получим приближение функции в окрестности некоторой точки ее касательной в этой точке.
Если оставить в разложении нулевой и первый члены ряда, то мы получим приближение функции в окрестности некоторой точки ее касательной в этой точке.

