Задачи с решениями

Длинная доска массой 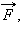M = 2 кг лежит на гладком горизонтальном столе. На доске находится брусок массой m = 1 кг. Коэффициент трения между бруском и доской μ = 0,2. К бруску приложена внешняя сила параллельная доске, модуль которой зависит от времени по закону F = βt, где β = 1,5 Н/с. Через какое время t₀ брусок начнет скользить по доске? Изобразите графически зависимость ускорений бруска и доски от времени.

Рассмотрим движение бруска и доски в инерциальной системе отсчета, связанной с Землей. На брусок в горизонтальном направлении действуют две силы: внешняя сила 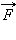и сила трения 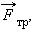направленная противоположно внешней силе. На доску действует только одна неуравновешенная сила 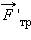– сила трения со стороны бруска, равная по третьему закону Ньютона 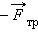(рис. 1.13.1).

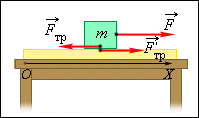Рисунок 1.13.1.

Силы тяжести доски и бруска уравновешены упругими силами реакции опор. Уравнения второго закона Ньютона, записанные в проекциях на ось 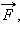OX, параллельную вектору силы имеют вид:

Здесь a₁ и a₂ – ускорения бруска и доски. Эти уравнения имеют смысл только при значениях a₁ ≥ a₂, так как по условию задачи доска не может двигаться быстрее бруска.

На первом этапе движения ускорения бруска и доски равны между собой: a₁ = a₂, следовательно

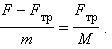
Предельное значение внешней силы F₀, при котором брусок и доска двигаются как единое целое, находится из условия

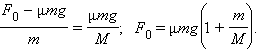
Здесь μmg – максимальное значение силы трения покоя. Внешняя сила достигает значения F₀ в момент времени t₀:

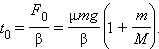
Подстановка числовых значений дает: t₀ = 2 с.

До момента времени t = t₀ ускорения обоих тел одинаковы и растут по линейному закону

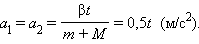
При t > t₀ ускорения бруска и доски будут разными:

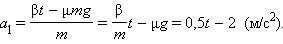
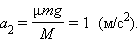
Графически зависимости ускорений бруска и доски от времени показаны на рис. 1.13.2.

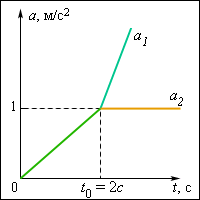Рисунок 1.13.2.

1 из 2