Глава 1. Механика

Задачи с решениямиЗадачи с решениямиВключить/Выключить фоновую музыкуВключить/Выключить звуки событий


Автомобиль массой m, мощность которого N, движется по горизонтальному участку дороги с коэффициентом трения μ. Через какой минимальный интервал времени после начала движения скорость автомобиля может достигнуть значения u?

Решение

Максимальная сила тяги автомобиля равна силе трения:

Fmax = μmg.

Время, в течение которого скорость автомобиля станет равной u, определится из выражения

где
Отсюда

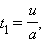
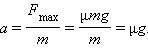
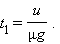
Однако такое решение может оказаться ошибочным, так как оно найдено в предположении, что автомобиль разгоняется под действием постоянной силы, равной максимальному значению силы трения покоя Fmax.

Такое предположение не противоречит условию задачи до тех пор, пока выполняется условие:

FmaxΔs ≤ NΔt,
где N – максимальная полезная мощность двигателя.

Преобразовав это выражение, получим:

откуда

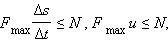
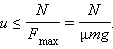
Следовательно, если

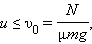
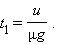
то минимальное время разгона автомобиля до скорости u равно

После достижения автомобилем скорости

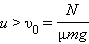
движение его с постоянным ускорением a = μg при постоянной мощности двигателя становится невозможным, так как изменение кинетической энергии автомобиля не может превышать работы, совершенной двигателем.

Если пренебречь потерями, то согласно теореме о кинетической энергии можно записать:

A = ΔEк,

откуда

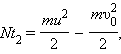
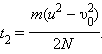
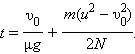
Таким образом, если после достижения автомобилем скорости υ0 мощность двигателя начинает использоваться полностью, то время, необходимое для достижения скорости u, большей υ0, будет складываться из времени, необходимого для достижения скорости υ0, и времени, которое нужно для увеличения скорости от значения υ0 до u:

Подставляя в это выражение значение скорости 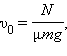получим:

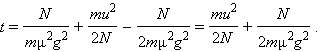
Следовательно, скорость автомобиля может возрастать пропорционально времени в первой степени до значения 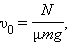а затем увеличиваться пропорционально времени в степени 1/2.


 2 из 2