Глава 1. Механика Задачи с решениями
Задачи с решениями

Два автомобиля приближаются к перекрестку по взаимно перпендикулярным дорогам с постоянными скоростями 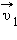 и
и 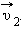 В момент времени, когда первый автомобиль достиг перекрестка, второй находился от него на расстоянии l0. Определите минимальное расстояние между автомобилями в процессе их движения. Проведите расчет при υ1 = 6 м/с, υ2 = 8 м/с, l0 = 30 м.
В момент времени, когда первый автомобиль достиг перекрестка, второй находился от него на расстоянии l0. Определите минимальное расстояние между автомобилями в процессе их движения. Проведите расчет при υ1 = 6 м/с, υ2 = 8 м/с, l0 = 30 м.
Решение
Первый способ.Положение каждого из автомобилей в любой момент времени можно задать двумя координатами. Выберем Землю в качестве тела отсчета. Направим координаты оси OX и OY вдоль дорог в направлении движения автомобилей (рис. 1.2.1). За начало координат выберем перекресток, за начало отсчета времени – момент пересечения перекрестка первым автомобилем. Уравнения движения автомобилей записываются в виде:
x1 = 0, y1 = υ1t,
x2 = l0 + υ2t, y2 = 0.
Расстояние l между автомобилями в любой момент времени равно

|
| Рисунок 1.2.1.
|
Задача сводится к нахождению минимального значения lmin переменной величины l, связанной функциональной зависимостью с другой переменной величиной t. Эта задача решается методами дифференциального исчисления. Однако, задачу можно решить гораздо проще, если выбрать другую систему отсчета.
Второй способ.В качестве тела отсчета выберем второй автомобиль; направление координатных осей O'X' и O'Y' и начало отсчета времени примем такими же, как и в первом способе решения задачи. В системе отсчета, связанной со вторым автомобилем, первый автомобиль движется со скоростью 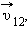 равной:
равной:
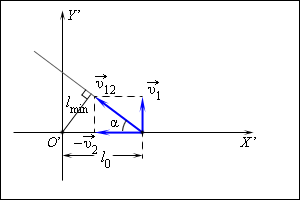
Эта скорость направлена под некоторым углом α к прямой, соединяющей автомобили в начальный момент времени t = 0 (рис. 1.2.2).
|
| Рисунок 1.2.2.
|
Кратчайшее расстояние lmin между автомобилями равно длине отрезка перпендикуляра, опущенного из начала координат, в котором находится второй автомобиль (точка O') на прямую, по которой движется первый автомобиль относительно второго.
Таким образом,
Подстановка числовых значений дает: lmin = 18 м.
 2 из 2
2 из 2
 |


 Задачи с решениями
Задачи с решениями

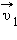 и
и 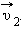 В момент времени, когда первый автомобиль достиг перекрестка, второй находился от него на расстоянии
В момент времени, когда первый автомобиль достиг перекрестка, второй находился от него на расстоянии 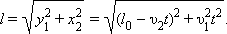

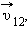 равной:
равной:
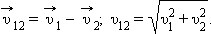

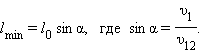
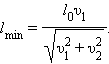
 2 из 2
2 из 2
