Глава 2. Механические колебания и волны

Задачи с решениямиЗадачи с решениямиВключить/Выключить фоновую музыкуВключить/Выключить звуки событий


Брусок, лежащий на горизонтальном столе, прикреплен горизонтальной пружиной к стене. Сначала пружина не деформирована. Затем брусок отодвинули от стены на расстояние x0 = 4,8 см и отпустили без начальной скорости. Принимая коэффициент трения между бруском и столом равным μ = 0,1, определите, какая часть первоначальной энергии пружины перейдет в тепло. Известно, что если брусок подвесить на этой пружине, то она растянется на a = 10 см.

Решение

По условию задачи

ka = mg,
где k – жесткость пружины. Обозначим последовательные максимальные отклонения бруска в обе стороны от положения недеформированной пружины через x0, x1, x2, ..., xn, xn+1, ... . Из-за трения каждое последовательное отклонение бруска меньше предыдущего:
xn+1 < xn.

Запишем закон сохранения и превращения энергии:

откуда

Таким образом, при каждом переходе через положение недеформированной пружины максимальное отклонение бруска от этого положения уменьшается на Δx = 2 см.

При наличии сухого трения возникает зона застоя, когда упругая сила пружины оказывается меньше по модулю максимальной силы трения μmg. Если брусок остановится в зоне застоя, то колебания прекратятся. Величина зоны застоя находится из условия

Таким образом, зона застоя, в пределах которой остановится брусок, равна

–1 см ≤ x ≤ 1 см.

В данной задаче x0 = 4,8 см, x1 = 2,8 см, x2 = 0,8 см < 1 см. Брусок остановится на расстоянии x2 = 0,8 см от положения недеформированной пружины. В этом положении потенциальная энергия пружины равна

По закону сохранения и превращения энергии в тепло перейдет энергия

а часть β энергии, перешедшая в тепло, окажется равной


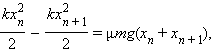
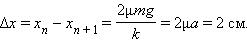
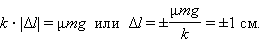
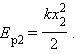
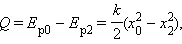
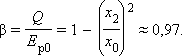
 2 из 2