Глава 3. Молекулярная физика и термодинамика
Молекулярно-кинетическая теория
3.7. Деформация
В твердых телах – аморфных и кристаллических – частицы (молекулы, атомы, ионы) совершают тепловые колебания около положений равновесия, в которых энергия их взаимодействия минимальна. При увеличении расстояния между частицами возникают силы притяжения, а при уменьшении – силы отталкивания (см. §3.1). Силы взаимодействия между частицами обусловливают механические свойства твердых тел.
Деформация твердого тела является результатом изменения под действием внешних сил взаимного расположения частиц, из которых состоит тело, и расстояний между ними.
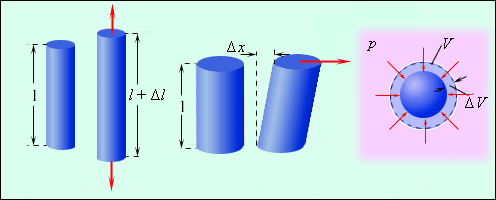
Существует несколько видов деформаций твердых тел. Некоторые из них представлены на рис. 3.7.1.
|
| Рисунок 3.7.1. Некоторые виды деформаций твердых тел: 1 – деформация растяжения; 2 – деформация сдвига; 3 – деформация всестороннего сжатия |
Простейшим видом деформации является деформация растяжения или сжатия. Ее можно характеризовать абсолютным удлинением Δl, возникающим под действием внешней силы 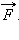 Связь между Δl и F зависит не только от механических свойств вещества, но и от геометрических размеров тела (его толщины и длины).
Связь между Δl и F зависит не только от механических свойств вещества, но и от геометрических размеров тела (его толщины и длины).
Отношение абсолютного удлинения Δl к первоначальной длине l образца называется относительным удлинением или относительной деформацией ε:
При растяжении ε > 0, при сжатии ε < 0.
Если принять направление внешней силы, стремящейся удлинить образец, за положительное, то F > 0 при деформации растяжения и F < 0 – при сжатии. Отношение модуля внешней силы F к площади S сечения тела называется механическим напряжением σ:
За единицу механического напряжения в СИ принят паскаль (Па). Механическое напряжение измеряется в единицах давления.
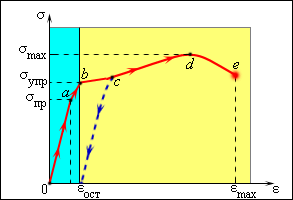
Зависимость между ε и σ является одной из важнейших характеристик механических свойств твердых тел. Графическое изображение этой зависимости называется диаграммой растяжения. По оси абсцисс откладывается относительное удлинение ε, а по оси ординат – механическое напряжение σ. Типичный пример диаграммы растяжения для металлов (таких как медь или мягкое железо) представлен на рис. 3.7.2.
|
| Рисунок 3.7.2. Типичная диаграмма растяжения для пластичного материала. Голубая полоса – область упругих деформаций |
При малых деформациях (обычно существенно меньших 1 %) связь между σ и ε оказывается линейной (участок Oa на диаграмме). При этом при снятии напряжения деформация исчезает. Такая деформация называется упругой. Максимальное значение σ = σпр, при котором сохраняется линейная связь между σ и ε, называется пределом пропорциональности (точка a). На линейном участке выполняется закон Гука:
Коэффициент E в этом соотношении называется модулем Юнга.
При дальнейшем увеличении напряжения связь между σ и ε становится нелинейной (участок ab). Однако при снятии напряжения деформация практически полностью исчезает, т. е. восстанавливаются размеры тела. Максимальное напряжение на этом участке называется пределом упругости .
Если σ > σупр, образец после снятия напряжения уже не восстанавливает свои первоначальные размеры и у тела сохраняется остаточная деформация εост. Такие деформации называются пластическими (участки bc, cd и de). На участке bc деформация происходит почти без увеличения напряжения. Это явление называется текучестью материала. В точке d достигается наибольшее напряжение σmax, которое способен выдержать материал без разрушения (предел прочности). В точке e происходит разрушение материала.
Материалы, у которых диаграмма растяжения имеет вид, показанный на рис. 3.7.2, называются пластичными. У таких материалов обычно деформация εmax, при которой происходит разрушение, в десятки раз превосходит ширину области упругих деформаций. К таким материалам относятся многие металлы.
Материалы, у которых разрушение происходит при деформациях, лишь незначительно превышающих область упругих деформаций, называются хрупкими (стекло, фарфор, чугун).
Аналогичным закономерностям подчиняется и деформация сдвига (рис. 3.7.1 (2)). В этом случае вектор силы 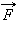 направлен по касательной к поверхности образца. Относительная деформация определяется безразмерным отношением Δx / l, а напряжение – отношением F / S (сила, действующая на единицу площади поверхности). При малых деформациях
направлен по касательной к поверхности образца. Относительная деформация определяется безразмерным отношением Δx / l, а напряжение – отношением F / S (сила, действующая на единицу площади поверхности). При малых деформациях
Коэффициент пропорциональности G в этом отношении называется модулем сдвига. Модуль сдвига для большинства твердых материалов в 2–3 раза меньше модуля Юнга. Например, у меди E = 1,1·1011 Н/м2, G = 0,42·1011 Н/м2. Следует помнить, что у жидких и газообразных веществ модуль сдвига равен нулю.
На рис. 3.7.1 (3) показана деформация всестороннего сжатия твердого тела, погруженного в жидкость. В этом случае механическое напряжение совпадает с давлением p в жидкости. Относительная деформация определяется как отношение изменения объема ΔV к первоначальному объему V тела. При малых деформациях
Коэффициент пропорциональности B в этой формуле называется модулем всестороннего сжатия.
Всестороннему сжатию могут подвергаться не только твердые тела, но и жидкости и газы. У воды B = 2,2·109 Н/м2, у стали B = 1,6·1011 Н/м2. На дне Тихого океана, на глубине порядка 4 км, давление p приблизительно равно 4·107 Н/м2. В этих условиях относительное изменение ΔV / V объема воды составляет 1,8 %, в то время как для стального тела оно составляет всего лишь 0,025 %, т. е. в 70 раз меньше. Твердые тела с их жесткой кристаллической решеткой значительно менее сжимаемы по сравнению с жидкостями, атомы и молекулы которых не так сильно связаны со своими соседями. Сжимаемость газов на много порядков выше, чем у жидкостей и твердых тел.
Величина модуля всестороннего сжатия определяет скорость звука в данном веществе (см. §2.7).







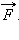 Связь между
Связь между 
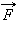 направлен по касательной к поверхности образца. Относительная деформация определяется безразмерным отношением
направлен по касательной к поверхности образца. Относительная деформация определяется безразмерным отношением 



