Декартовы координаты

Задачи с решениямиЗадачи с решениямиВключить/Выключить фоновую музыкуВключить/Выключить звуки событий


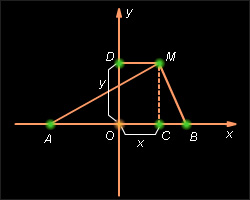Доказать, что множество точек M плоскости таких, что сумма расстояний от них до данных точек A и B равна числу 2a > AB, есть эллипс с фокусами в точках A и B.

Решение

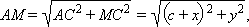
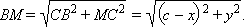
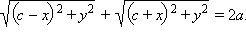Выберем прямоугольную систему координат Oxy так, чтобы ось Ox совпала с прямой AB, а начало координат с серединой отрезка AB (см. рис) Тогда точка A имеет координаты (–c, 0), а точка B – (c, 0), где c > 0. Пусть M (x, y) такая точка плоскости, что AM + MB = 2a. Из рисунка видно, что


Имеем Перенося второе слагаемое в правую часть и возводя обе части в квадрат получим 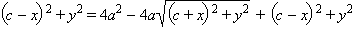или 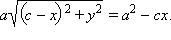Возводя еще раз обе части равенства в квадрат получим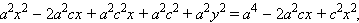
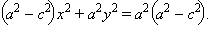откуда Так как 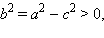a > c по условию, то то уравнение можно записать в виде 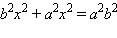или 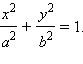Это каноническо уравнение эллипса, фокусы которого 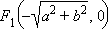и 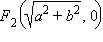совпадают по выбору системы координат с точками A и B.


 15 из 24