

 Задачи с решениями
Задачи с решениями

Используя векторы, доказать, что в любом треугольнике медианы пересекаются в одной точке, которая делит каждую медиану в отношении
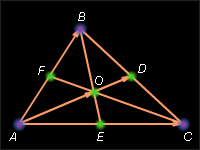 |
Пусть дан треугольник 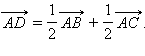 Но точка
Но точка 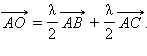
Аналогично, 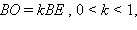
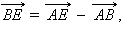
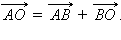 Отсюда
Отсюда 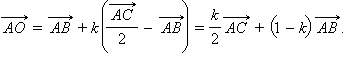 С учетом ранее полученного выражения для
С учетом ранее полученного выражения для 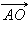 имеем равенство
имеем равенство 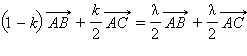 или
или 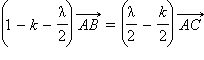 Но
Но 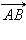 и
и 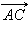 не коллинеарны и равенство возможно лишь при при одновременном выполнении равенств
не коллинеарны и равенство возможно лишь при при одновременном выполнении равенств 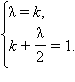 Отсюда
Отсюда 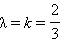 и, следовательно,
и, следовательно, 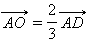 и
и 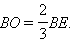 Заменив в рассуждениях медиану
Заменив в рассуждениях медиану 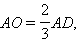
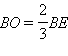 и
и 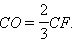
 11 из 25
11 из 25
 |