Площадь Задачи с решениями
Задачи с решениями

Доказать, что площадь треугольника может быть вычислена по следующим формулам:
а)
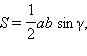 где γ – угол между сторонами a и b треугольника;
где γ – угол между сторонами a и b треугольника;
б) 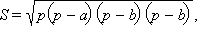 где a, b, c – стороны треугольника, а
где a, b, c – стороны треугольника, а
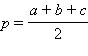 – полупериметр;
– полупериметр;
в)
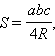 где a, b, c – стороны треугольника, R – радиус описанной окружности;
где a, b, c – стороны треугольника, R – радиус описанной окружности;
г) S = pr, где p – полупериметр треугольника, r – радиус вписанной окружности.
Решение
а) Проведем в треугольнике ABC высоту BD. Имеем
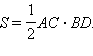 Из прямоугольного треугольника CBD: BD = BC · sin γ, если γ острый (см. первый рисунок), BD = BC · sin (180° – γ), если угол γ тупой (см. второй рисунок). Так как sin (180° – γ) = sin γ, то в любом случае BD = BC · sin γ.
Из прямоугольного треугольника CBD: BD = BC · sin γ, если γ острый (см. первый рисунок), BD = BC · sin (180° – γ), если угол γ тупой (см. второй рисунок). Так как sin (180° – γ) = sin γ, то в любом случае BD = BC · sin γ.
Cледовательно,
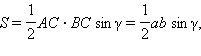 что и требовалось доказать.
что и требовалось доказать.
б) Из пункта а)
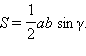 По теореме косинусов
По теореме косинусов 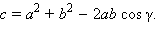 Отсюда
Отсюда
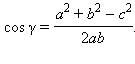 Значит,
Значит,
Замечая, что a + b + c = 2p, a + b – c = 2p – 2c, a + c – b = 2p – 2b, c – a + b = 2p – 2a, получаем
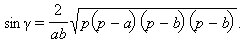 Таким образом,
Таким образом,
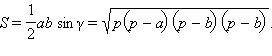
в) Как известно (см. задачу 1 главы 7),
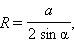 где α – угол, противолежащей стороне a треугольника. Отсюда
где α – угол, противолежащей стороне a треугольника. Отсюда
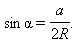 Умножая обе части на
Умножая обе части на
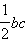 и замечая, что
и замечая, что
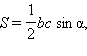 получаем
получаем
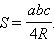
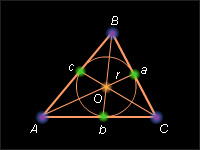
г) Соединим центр вписанной окружности O с вершинами треугольника ABC и проведем радиусы в точки касания (см. третий рисунок).
Площадь треугольника ABC равна сумме площадей треугольников OAB, OBC и AOC. Но
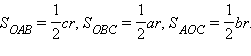 Отсюда
Отсюда
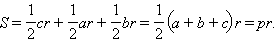
 1 из 6
1 из 6
 |


 Задачи с решениями
Задачи с решениями

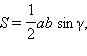 где
где 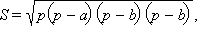 где
где 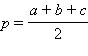 – полупериметр;
– полупериметр; 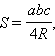 где
где 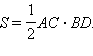 Из прямоугольного треугольника
Из прямоугольного треугольника 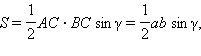 что и требовалось доказать.
что и требовалось доказать.
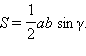 По теореме косинусов
По теореме косинусов 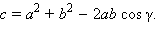 Отсюда
Отсюда
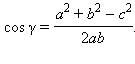 Значит,
Значит,
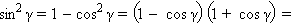
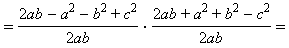
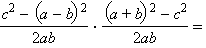
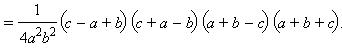
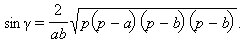 Таким образом,
Таким образом,
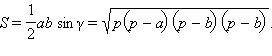
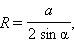 где
где 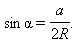 Умножая обе части на
Умножая обе части на
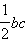 и замечая, что
и замечая, что
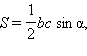 получаем
получаем
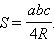
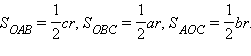 Отсюда
Отсюда
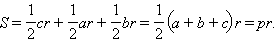
 1 из 6
1 из 6
