Окружность Задачи с решениями
Задачи с решениями

Доказать, что в любом треугольнике отношение длины стороны к синусу противолежащего угла равно диаметру описанной около треугольника окружности.
Решение
Пусть ABC – данный треугольник, и угол при вершине A равен α, противолежащая сторона равна a, w (O, R) – окружность, описанная около треугольника ABC (см. рисунки). Проведем диаметр BD. По свойству углов, вписанных в окружность, угол при вершине D прямоугольного треугольника BCD (угол BCD опирается на диаметр окружности w (O, R)) равен либо α, если точки A и D лежат по одну сторону от прямой BC (см. первый рисунок), либо (180° – α), если они лежат по разные стороны от прямой BC (см. второй рисунок). В первом случае BC = BD sin α, во втором BC = BD sin (180° – α) = BD sin α. Таким образом, в обоих случаях a = 2R sin α. Следовательно,
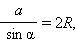 что и требовалось доказать.
что и требовалось доказать.
 1 из 6
1 из 6
 |


 Задачи с решениями
Задачи с решениями

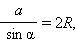 что и требовалось доказать.
что и требовалось доказать.
 1 из 6
1 из 6
