

 |
 |
Самостоятельная работа.
Изучение чертежей учащимися будет эффективным, если учитель сможет организовать самостоятельную работу каждого из них по сопоставлению свойств пространственной фигуры и особенностей ее чертежа. Для этой цели оказываются удобными дидактические печатные материалы с заданными чертежами, вопросами к ним и наборами возможных ответов (требуется указать лишь номера верных ответов). Такая форма обеспечивает интенсивную самостоятельную работу учащихся на уроках и быстрое коллективное обсуждение правильности полученных ответов.
Приведем несколько таких текстов:
Работа № 1 (Рисунок H.4.1.7.1).

|
| Рисунок M.3.3.1 |
Работа № 2 (Рисунок H.4.1.7.2).

|
| Рисунок M.3.3.2 |
Работа № 3 (Рисунок H.4.1.7.3. ![]() ABC
ABC

|
| Рисунок M.3.3.3 |
Какие прямые образуют угол?
1)
Сколько углов сходится в вершине
1) Один.
2) Два.
3) Три.
4) Ни один из этих ответов не верен.
Какой угол лежит в плоскости?
1) ![]() BCC
BCC
2) ![]() BCA
BCA
3) ![]() C
C
4) 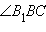 .
.
Укажите взаимно перпендикулярные прямые:
1)
2)
3)
4)
Укажите неперпендикулярные друг другу прямые:
1)
2)
3)
4)
Кроме выборочной формы ответа, полезны также задания, в которых ученику приходится конструировать ответ самому. Эти задания рационально «привязывать» к имеющимся чертежам. Например, при рассмотрении предыдущего чертежа уместно на уроке дополнительно рассмотреть с учащимися следующие вопросы:
Если работать в системе, то все это по силам ученикам 7–9 класса, кроме того, осуществляется межпредметная связь с черчением.
Но более удачно и эффективнее здесь применение интерактивных моделей из курса «Открытая Математика 2.5. Стереометрия». Роль средств наглядности возрастает в связи с трехмерностью изучаемых в стереометрии объектов, которая порождает условность их изображения на чертежах. Интерактивные модели, с одной стороны, обеспечивают предъявление учащимся объемных моделей, с другой стороны могут демонстрировать соответствующие им плоские чертежи. Установление соответствия между элементами объемных и плоских моделей позволяют выполнять модели и трехмерные чертежи курса.
Использование моделей в преподавании геометрии должно помогать абстрактному мышлению ученика, развивать его. Плоского чертежа или тем более словесного описания недостаточно.
Интерактивные модели – очень важное средство наглядности, позволяющее решать многие проблемы обучения. Иллюзия трехмерности, создаваемая на экране позволяет сразу ввести учащихся в курс стереометрии. При этом учащиеся могут видеть не только сами стереометрические тела, но и следить за ходом рассуждений, проникая, в частности, в идейный смысл курса.
 |
 |
 |