Модель 10.2. Отрезок на координатной плоскости

Глава 10. Декартовы координаты

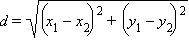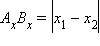Если вершины отрезка AB имеют координаты A(x₁; y₁) и B (x₂; y₂), то верны следующие соотношения:

Длина отрезка AB равняется .
Длина проекции отрезка AB на ось x равняется , на ось y: .
Координаты середины отрезка S вычисляются по формулам , .
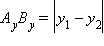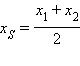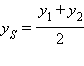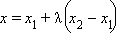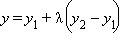Координаты любой точки C отрезка подчиняются равенствам , , где λ – некоторое действительное число. При этом для любой λ из отрезка [0; 1] существует соответствующая ей точка на отрезке AB.

В интерактивной модели вершины A и B отрезка AB можно перемещать по плоскости либо мышью, либо изменяя координаты этих точек в полях числового ввода. Точку S можно перемещать вдоль отрезка либо мышью, либо изменяя значения параметра λ (от 0 до 1) в поле числового ввода.

Убедитесь, изменяя взаимное расположение точек A, B и S в справедливости указанных соотношений.

Переключившись в демонстрационный режим при помощи кнопки со значком кинопроектора, можно просмотреть анимацию. Кнопка Старт запускает ее, кнопка Стоп – приостанавливает, а кнопка Сброс возвращает анимацию в исходное состояние. Кнопка со значком руки переводит модель обратно в интерактивный режим.