Модель 7.2. Параллелограмм

Глава 7. Четырехугольник

Параллелограммом называется четырехугольник, у которого противолежащие стороны попарно параллельны. Высотой параллелограмма, проведенной к данной его стороне, называется перпендикуляр, опущенный из произвольной точки противолежащей стороны к прямой, содержащей данную сторону.

Параллелограмм обладает следующими свойствами:

Противолежащие стороны параллелограмма равны, противолежащие углы также равны.
Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
Площадь параллелограмма равна произведению его стороны на проведенную к ней высоту. Кроме того, .

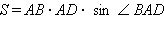Интерактивная модель демонстрирует указанные свойства параллелограмма. В центральном окне изображен параллелограмм ABCD, точки B и D можно перетаскивать при помощи мыши. Компьютер рассчитывает и выводит на экран длины сторон параллелограмма, градусные меры углов, а также его площадь. Установив флажок в выключателе Диагонали, можно посмотреть длину диагоналей и длины отрезков, на которые диагонали делятся точкой пересечения. По флажку Высота можно посмотреть длины всех высот параллелограмма.

Выключатель Прямоугольник превращает параллелограмм в прямоугольник. Прямоугольником называется параллелограмм, у которого все углы прямые. Диагонали прямоугольника ABCD равны, а площадь S = AB · CD.

Выключатель Ромб превращает параллелограмм в ромб – параллелограмм, у которого все стороны равны. Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов.

Если отмечены оба выключателя (и Прямоугольник, и Ромб), то параллелограмм превращается в квадрат. У квадрата все стороны равны, а все углы прямые. Диагонали квадрата равны и пересекаются под прямым углом. Площадь S квадрата ABCD S = AB².

Переключившись в демонстрационный режим при помощи кнопки со значком кинопроектора, можно просмотреть анимацию. Кнопка Старт запускает ее, кнопка Стоп – приостанавливает, а кнопка Сброс возвращает анимацию в исходное состояние. Кнопка со значком руки переводит модель обратно в интерактивный режим.