Глава 6. Окружность

Модель 6.3.  Касательные и секущие

Прямая, имеющая единственную точку с окружностью, называется касательной. Общая точка окружности и касательной называется точкой касания. Радиус, проведенный в точку касания, перпендикулярен касательной. Прямая, пересекающая окружность в двух точках, называется секущей.

Пусть из точки P вне окружности проведены два луча, пересекающие окружность в точках A, B и C, D соответственно. Тогда

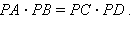
В интерактивной модели показана окружность и две ее касательных PB и PD. Потянув мышью за точку P, можно изменить ее расположение относительно окружности. Перемещая мышью точки A либо B и C либо D, можно изменять взаимное расположение секущих.

Убедитесь, что указанное равенство выполняется при любом взаимном расположении секущих.

Модель демонстрирует и другую теорему, посвященную секущим: градусная мера угла между секущими равна полуразности дуг, лежащих в данном плоском угле. Математически это тождество записывается так: .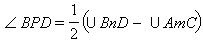

Установив флажок в выключателе Касательная, можно одну из секущих превратить в касательную. В этом случае модель демонстрирует теорему о касательной и секущей, согласно которой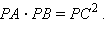

Переключившись в демонстрационный режим при помощи кнопки со значком кинопроектора, можно просмотреть анимацию. Кнопка Старт запускает ее, кнопка Стоп – приостанавливает, а кнопка Сброс возвращает анимацию в исходное состояние. Кнопка со значком руки переводит модель обратно в интерактивный режим.