Перпендикулярность прямых и плоскостей Задачи с решениями
Задачи с решениями

Найти угол между апофемой боковой грани и соседней боковой гранью треугольной пирамиды, все ребра которой равны (апофемой боковой грани правильной треугольной пирамиды называется высота этой грани, проведенная из вершины пирамиды).
Решение
Шаг 1
Основанием данной пирамиды является равносторонний треугольник. Поскольку все боковые ребра пирамиды равны между собой, ее высота проходит через центр основания. Значит, данная пирамида правильная. На рисунке показано ее изображение. PD – апофема грани PBC. Найдем угол между прямой PD и плоскостью боковой грани PAC.
Шаг 2
Угол между наклонной и плоскостью – это угол между наклонной и ее ортогональной проекцией на эту плоскость. Значит, нужно спроектировать прямую PD на плоскость PAC. Поскольку точка P лежит в плоскости PAC, нужно спроектировать точку D на плоскость PAC.
Шаг 4
Действуем по правилу, описанному в шаге третьем. Проводим перпендикуляр DF из точки D на прямую AC (DF || BE). В плоскости PAC проведем перпендикуляр FG к прямой AC. Теперь проводим из точки D перпендикуляр DH к прямой FG. DH – перпендикуляр к плоскости PAC. Значит, H = ПрPACD и DPH – искомый угол.
Шаг 5
Пусть AB = a. DF – средняя линия ΔCBE, значит,
Из прямоугольного
ΔDFH имеем:
DH = DF sin DFH
DFH (1). Заметим, что
BE = PE,
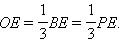
Поэтому
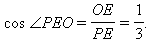
Очевидно,
 DFH =
DFH = OEP
OEP. Из равенства (1) находим:
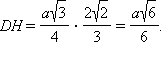
Из прямоугольного
ΔDPH находим искомый угол
DPH:
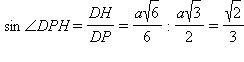
и
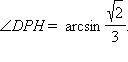
Ответ:
 16 из 19
16 из 19
 |


 Задачи с решениями
Задачи с решениями

 16 из 19
16 из 19
