Перпендикулярность прямых и плоскостей Задачи с решениями
Задачи с решениями

В треугольной пирамиде DABC грань ACD – правильный треугольник со стороной a, грань ABC – равнобедренный прямоугольный треугольник с прямым углом C. Известно, что BD = b. Найти величину двугранного угла AC.
Решение
Шаг 1
Изобразим треугольную пирамиду DABC и произведем маркировку рисунка. Согласно условию DA = DC = AC = BC = a, BD = b. Легко найти и ребро AB. Поскольку треугольник ABC прямоугольный и равнобедренный, AB – его гипотенуза, то
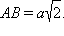
Шаг 2
Для нахождения величины двугранного угла AC нужно построить его линейный угол. Проведем через точку D плоскость, перпендикулярную прямой AC. Для этого проводим высоту DE в треугольнике DAC. Она же является медианой этого треугольника, поскольку он правильный. AE = CE.
Теперь проводим из точки E перпендикуляр к стороне AC до пересечения в точке F со стороной AB. Плоскость DEF перпендикулярна ребру AC двугранного угла, значит, DEF – линейный угол этого двугранного угла.
Шаг 3
Как же найти величину угла DEF? Обычно угол находят из некоторого треугольника. Рассмотрим треугольник DEF.
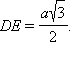 EF – средняя линия ΔABC, поэтому
EF – средняя линия ΔABC, поэтому
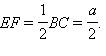 Остается найти DF. Заметим, что DF – медиана ΔABD.
Остается найти DF. Заметим, что DF – медиана ΔABD.
Шаг 4
Вынесем треугольник ABD во фронтальную плоскость. Продлим отрезок DF на расстояние FG = DF. Четырехугольник ADBG – параллелограмм, т. к. его диагонали, пересекаясь, делятся пополам. Известно, что сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон. Значит, DG2 + AB2 = 2AD2 + 2BD2 или
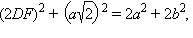 4DF2 = 2b2,
4DF2 = 2b2,
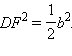
Шаг 5
Из ΔDEF согласно теореме косинусов получаем
Ответ:
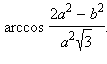
 18 из 19
18 из 19
 |


 Задачи с решениями
Задачи с решениями

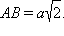
 18 из 19
18 из 19
