Многогранники Задачи с решениями
Задачи с решениями

В правильной четырехугольной пирамиде (см. рисунок) двугранный угол при ребре основания равен β, а сторона основания – a. Через ребро основания проведена плоскость под углом γ (0 < γ < β) к плоскости основания. Найти площадь сечения.
Решение
Имеем: PE и PF – апофемы пирамиды,  PEF = β по условию, AB = a. В плоскости PEF проведем отрезок EK так, что
PEF = β по условию, AB = a. В плоскости PEF проведем отрезок EK так, что  KEF = γ. Через точку K проведем отрезок MN || DC. Плоскость AMNB составляет с плоскостью основания пирамиды угол γ. В сечении имеем трапецию AMNB, площадь которой
KEF = γ. Через точку K проведем отрезок MN || DC. Плоскость AMNB составляет с плоскостью основания пирамиды угол γ. В сечении имеем трапецию AMNB, площадь которой
Из ΔKEF по теореме синусов имеем
Из прямоугольного треугольника POF (PO – высота пирамиды) находим
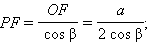 из подобия ΔPMN и ΔPDC запишем соотношения
из подобия ΔPMN и ΔPDC запишем соотношения
откуда
Теперь из равенства (*) имеем
Ответ:
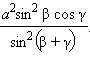
 13 из 14
13 из 14
 |


 Задачи с решениями
Задачи с решениями

![]() PEF = β
PEF = β![]() KEF = γ
KEF = γ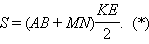
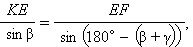 откуда
откуда
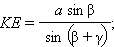
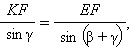 откуда
откуда
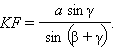
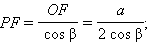 из подобия
из подобия 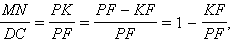
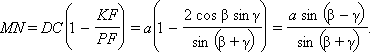
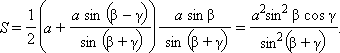
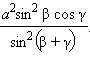
 13 из 14
13 из 14
