|
|
Выпуклый многогранник называется вписанным, если все его вершины лежат на некоторой сфере. Эта сфера называется описанной для данного многогранника.
Выпуклый многогранник называется описанным, если все его грани касаются некоторой сферы. Эта сфера называется вписанной для данного многогранника.
При рассмотрении понятий вписанной и описанной сферы обнаруживается аналогия с понятием вписанной и описанной окружности. Однако, если в любой треугольник можно вписать окружность и около любого треугольника можно описать окружность, то не всякий многогранник является вписанным или описанным. Несмотря на это, оказывается, что пространственный аналог треугольника – треугольная пирамида, тем не менее, всегда имеет единственную вписанную и описанную сферу. Докажем это.
Треугольная пирамида имеет единственную описанную сферу.
Треугольная пирамида имеет единственную вписанную сферу.
Для того, чтобы пирамида была вписанной в сферу, необходимо и достаточно, чтобы ее основанием был вписанный в окружность многоугольник.
Любая правильная пирамида является вписанной.
Пусть центр сферы, описанной вокруг пирамиды, лежит на прямой, проходящей через высоту пирамиды. Тогда
где
Если сфера вписана в многогранник, то объем этого многогранника равен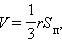 
где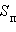 
– площадь полной поверхности многогранника,
Поскольку центр вписанной сферы одинаково удален от всех граней многогранника, он лежит на пересечении биссекторных плоскостей всех двугранных углов многогранника.
В правильную
|
|
 |
