Тела вращения
Задачи с решениями
В равностороннем цилиндре высота равна диаметру оснований, центры оснований – O1 и O. На окружностях оснований взяты точки A, B, так, что угол между прямыми O1A и OB равен α. Найти угол между осью цилиндра и прямой AB.
Решение
Шаг 1
Изображаем цилиндр с осью OO1. На верхнем основании проводим радиус O1A, а на нижнем – OB. По условию угол между скрещивающимися прямыми O1A и OB равен α. Проведем в верхнем основании радиус O1C || OB. Согласно определению угла между скрещивающимися прямыми 
AO1C = α.
Шаг 2
Прямые AB и OO1 скрещиваются. Проводим образующую BC. Согласно определению угла между скрещивающимися прямыми ABC – это угол между осью цилиндра OO1 и прямой AB. Пусть ABC = x.
Шаг 3
Пусть радиус цилиндра равен R. Учитывая, что данный цилиндр равносторонний, имеем: OO1 = BC = 2R.
Шаг 5
Из прямоугольного ΔABC имеем:
Ответ:
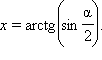
3 из 18
 |
Из прямоугольного 
