

 |
 |
Рассмотрим произвольную точку 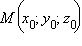 и некоторый вектор
и некоторый вектор 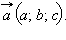 Поставим задачу найти множество точек
Поставим задачу найти множество точек 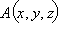 таких, что вектор
таких, что вектор 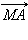 параллелен вектору
параллелен вектору 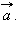 Очевидно, что искомое множество – прямая, проходящая через точку
Очевидно, что искомое множество – прямая, проходящая через точку 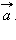

Найдем уравнение этого геометрического места точек. Параллельность векторов 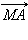 и
и 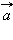 означает, что существует такое число
означает, что существует такое число 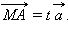 Пусть вектор
Пусть вектор 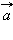 имеет координаты
имеет координаты
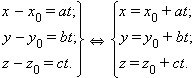 |
Три последних равенства и описывают прямую в пространстве, проходящую через заданную точку параллельно направляющему вектору. Заметим, что в этих равенствах
Прямую в пространстве можно также задать системой двух линейных уравнений, в которых переменными являются координаты
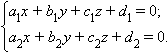 |
 |
 |
 |

