Глава M. Методика
M.3. Методика работы с компьютерным курсом
M.3.5. Примерные контрольные работы по учебным пособиям А. В. Погорелова, Л. С. Атанасяна
Примерная контрольная. Тема «Параллельность прямых» 10 класс. По Л. С. Атанасяну
Вариант 1.
-
Основание AD трапеции ABCD лежит в плоскости a. Через точки B и C проведены параллельные прямые, пересекающие плоскость а в точках E и F соответственно.
-
Каково взаимное расположение прямых EF и AB?
-
Чему равен угол между прямыми EF и AB, если ABC = 150°? Ответ обоснуйте.
-
Дан пространственный четырехугольник ABCD, в котором диагонали AC и BD равны. Середины сторон этого четырехугольника соединены последовательно отрезками.
Вариант 2.
-
Треугольники ABC и ADC лежат в разных плоскостях и имеют общую сторону AC. Точка P – середина стороны AD, точка K – середина DC.
-
Каково взаимное расположение прямых PK и AB?
-
Чему равен угол между прямыми PK и AB, если ABC = 40° и BCA = 80°? Ответ обоснуйте.
-
Дан пространственный четырехугольник ABCD, M и N – середины сторон AB и BC соответственно, E  CD, K
CD, K  DA, DE : EC = 1 : 2, DK : KA = 1 : 2.
DA, DE : EC = 1 : 2, DK : KA = 1 : 2.
-
Выполните рисунок к задаче.
-
Докажите, что четырехугольник MNEK – трапеция.
Примерная контрольная работа. Тема «Параллельность прямых» 10 класс. По А. В. Погорелову
Вариант 1.
-
Точки K, M, P, T не лежат в одной плоскости. Могут ли прямые KM и PT пересекаться?
-
Через точки A, B и середину M отрезка AB проведены параллельные прямые, пересекающие некоторую плоскость ось в точках A, B, M соответственно. Найдите длину отрезка MM, если AA1 = 13 м, BB1 = 7 м, причем отрезок AB не пересекает плоскость a.
-
Точка P не лежит в плоскости трапеции ABCD с основаниями AD и BC. Докажите, что прямая, проходящая через середины отрезков PB и PC, параллельна средней линии трапеции.
Вариант 2.
-
Прямые EN и KM не лежат на одной плоскости. Могут ли прямые EM и NK пересекаться? (Ответ обоснуйте).
-
Через точки A, B и середину M отрезка AB проведены параллельные прямые, пересекающие некоторую плоскость а в точках A1, B1, M1 соответственно. Найдите длину отрезка MM1, если AA1 = 3 м, BB1 =17 м, причем отрезок AB не пересекает плоскость a.
-
Точка E не лежит в плоскости параллелограмма ABCD. Докажите, что прямая, проходящая через середины отрезков EA и EB, параллельна стороне CD параллелограмма.
Контрольная работа. Тема: «Параллельность прямых и плоскостей». 10 класс. По Л. С. Атанасяну
Вариант 1.
-
Прямые a и b лежат в параллельных плоскостях α и β. Могут ли эти прямые быть:
-
параллельными;
-
скрещивающимися?
Сделайте рисунок для каждого возможного случая.
-
Через точку O, лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках A1 и A2 соответственно, прямая m – в точках B1, и B2. Найдите длину отрезка A2B2, если A1B1= 12 cм, OB1 : OB2 = 3 : 4.
-
Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью, проходящей через точки M, N и K, являющиеся серединами ребер AB, BC и DD1.
Вариант 2.
-
Прямые a и b лежат в пересекающихся плоскостях α и β. Могут ли эти прямые быть:
-
параллельными;
-
скрещивающимися?
Сделайте рисунок для каждого возможного случая.
-
Через точку O, не лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках A1 и A2 соответственно, прямая m – в точках B1 и B2. Найдите длину отрезка A1B1, если A2B2 = 15 cм.
-
Изобразите тетраэдр DABC и постройте его сечение плоcкостью, проходящей через точки M и N, являющиеся серединами ребер DC и BC, и точку K, такую, что K  DA, AK : KD =1 : 3.
DA, AK : KD =1 : 3.
Примерная контрольная работа. Тема «Многогранники» По А. С. Атанасяну
Вариант 1.
-
Основанием пирамиды DABC является правильный треугольник ABC, сторона которого равна a. Ребро DA перпендикулярно к плоскости ABC, а плоскость DBC составляет с плоскостью ABC угол 30°. Найдите площадь боковой поверхности пирамиды.
-
Основанием прямого параллелепипеда ABCDA1B1C1D1 является ромб ABCD, сторона которого равна a и угол равен 60°. Плоскость A1D1C1 составляет с плоскостью основания угол 60°. Найдите:
Вариант 2.
-
Основанием пирамиды MABCD является квадрат ABCD, ребро MD перпендикулярно к плоскости основания, AD = DM = a. Найдите площадь поверхности пирамиды.
-
Основанием прямого параллелепипеда 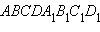 является параллелограмм ABCD, стороны которого равны
является параллелограмм ABCD, стороны которого равны 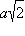 и 2a, острый угол равен 45°. Высота параллелепипеда равна меньшей высоте параллелограмма. Найдите:
и 2a, острый угол равен 45°. Высота параллелепипеда равна меньшей высоте параллелограмма. Найдите:
-
меньшую высоту параллелограмма;
-
угол между плоскостью ABC и плоскостью основания;
-
площадь боковой поверхности параллелепипеда;
-
площадь поверхности параллелепипеда.
Примерная контрольная работа. Тема «Призма. Параллелепипед» 11 класс. По А. В. Погорелову
Вариант 1.
-
Найдите высоту правильной шестиугольной призмы (можно дать обозначение призмы: ABCDEHA1B1C1D1E1H1), если сторона ее основания равна a, а меньшая из диагоналей – b.
-
Найдите сторону основания и высоту правильной четырехугольной призмы, если площадь ее полной поверхности равна 40 см2, а боковая поверхность – 32 см2.
-
В прямом параллелепипеде с высотой 14 м стороны основания ABCD равны 3 м и 4 м, диагональ AC = 6 м. Найдите площадь диагонального сечения параллелепипеда, проходящего через вершины B и D.
Вариант 2.
-
Найдите высоту правильной шестиугольной призмы, если сторона ее основания равна a, а большая из диагоналей – b.
-
Найдите сторону основания и высоту правильной четырехугольной призмы, если ее боковая поверхность равна 8 см2, а полная – 40 см2.
-
В прямом параллелепипеде с высотой 15 м стороны основания ABCD равны 2 м и 4 м, диагональ AC = 5 м. Найдите площадь диагонального сечения параллелепипеда, проходящего через вершины B и D.




![]() CD
CD![]() DA
DA![]() DA
DA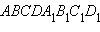 является параллелограмм
является параллелограмм 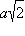 и
и 

