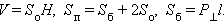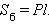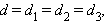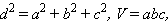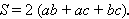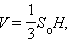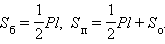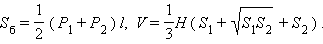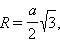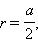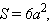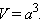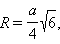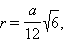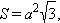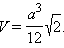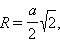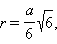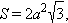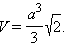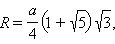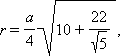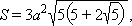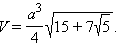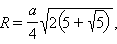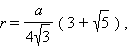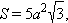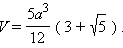Справочник
R.1. Основные формулы
R.1.2. Многогранники
Призма.
Обозначения:
l – боковое ребро, P – периметр основания, 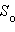 – площадь основания, H – высота,
– площадь основания, H – высота, 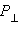 – периметр перпендикулярного сечения, Sб – площадь боковой поверхности, Sп – площадь полной поверхности призмы, V – объем.
– периметр перпендикулярного сечения, Sб – площадь боковой поверхности, Sп – площадь полной поверхности призмы, V – объем.
У прямой призмы
Параллелепипед.
Обозначения:
a, b, c – измерения, d1, d2, d3 – диагонали, V – объем, S – площадь полной поверхности.
Для прямого параллелепипеда:
Пирамида.
Обозначения:
P – периметр основания, l – апофема, H – высота, Sо – площадь основания, Sб – площадь боковой поверхности, Sп – площадь полной поверхности, V – объем пирамиды. В общем случае площадь боковой поверхности пирамиды равна сумме площадей ее боковых граней.
Для правильной пирамиды:
Усеченная пирамида.
Обозначения:
P1, P2 – периметры оснований, l – апофема, H – высота, S1, S2 – площади оснований, V – объем, Sб – площадь боковой поверхности для правильной пирамиды.
Правильные многогранники.
Обозначения:
a – ребро, H – высота, S – площадь поверхности, V – объем, R – радиус описанной сферы, r – радиус вписанной сферы.
Куб. Все шесть граней – квадраты. Имеет восемь вершин и двенадцать ребер.
Тетраэдр. Все четыре грани – равносторонние треугольники. Имеет четыре вершины и шесть ребер.
Октаэдр. Все восемь граней – равносторонние треугольники. Имеет шесть вершин и двенадцать ребер.
Додекаэдр. Все двенадцать граней – правильные пятиугольники. Имеет двадцать вершин и тридцать ребер.
Икосаэдр. Все двадцать граней – равносторонние треугольники. Имеет двенадцать вершин и тридцать ребер.






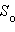 – площадь основания,
– площадь основания, 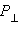 – периметр перпендикулярного сечения,
– периметр перпендикулярного сечения,