Глава 9. Координаты и векторы в пространстве

Модель 9.1.  Векторы в пространстве

Вектор – направленный отрезок. Длиной (модулем) 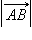ненулевого вектора 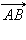называется длина отрезка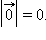 AB. Длина нулевого вектора равна нулю:

Суммой двух векторов и 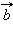называется новый вектор 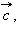который обозначается 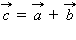и получается следующим образом. Отложим от произвольной точки 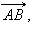A вектор равный 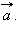Теперь от точки B отложим вектор равный 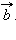Вектор 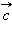и называется суммой векторов 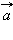и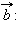   

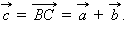
Для любых векторов 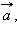  и 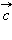справедливы равенства:

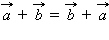• (переместительный закон);
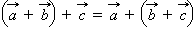• (сочетательный закон).

Разностью векторов 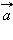и 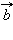называется такой вектор 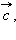сумма которого с вектором 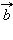равна вектору 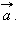Обозначается разность векторов так: 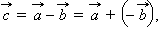где – вектор, противоположный вектору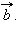

Скалярным произведением векторов 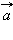и 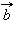называется произведение их длин на косинус угла между ними:

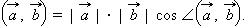Скалярное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны. Скалярный квадрат вектора, т. е. скалярное произведение его самого на себя, равен квадрату его длины. Скалярное произведение двух векторов 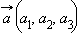и 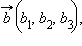заданных своими координатами, может быть вычислено по формуле: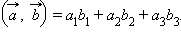

В модели можно задать координаты двух векторов в пространстве. В окне вывода показываются длина каждого вектора, их сумма, разность и скалярное произведение.

Переключившись в демонстрационный режим при помощи кнопки со значком кинопроектора, можно просмотреть анимацию. Кнопка Старт запускает ее, кнопка Стоп – приостанавливает, а кнопка Сброс возвращает анимацию в исходное состояние. Кнопка со значком руки переводит модель обратно в интерактивный режим.