

 |
 |
Рассмотрим выражение вида:
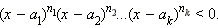 |
(1) |
Основным методом решения неравенств вида (1) является метод интервалов. Начнём рассматривать его, прежде всего, для многочленов. Этот метод основан на том, что двучлен
Отсюда следуют полезные замечания.
Многочлен 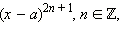 то есть двучлен в нечётной степени, положителен и отрицателен на тех же интервалах, что и
то есть двучлен в нечётной степени, положителен и отрицателен на тех же интервалах, что и
Многочлен 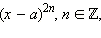 то есть двучлен в чётной степени, не меняет знак при переходе через точку
то есть двучлен в чётной степени, не меняет знак при переходе через точку
Вывод. Многочлены вида 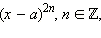 при решении строгих неравенств («<» или «>») можно опустить, так как они не влияют на знак неравенства. При этом из решения нужно исключить точки, в которых многочлен равен нулю:
при решении строгих неравенств («<» или «>») можно опустить, так как они не влияют на знак неравенства. При этом из решения нужно исключить точки, в которых многочлен равен нулю: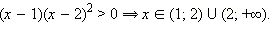
Многочлен 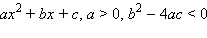 всегда положителен и потому при решении любого неравенства может быть опущен.
всегда положителен и потому при решении любого неравенства может быть опущен.
При переходе через точку

 |
|
Модель 3.7.
Метод интервалов
|
 |
 |
|
 |
 |
|
Рассмотрим стандартный приём решения рациональных неравенств, основанный на сведении данного неравенства к неравенству для многочлена, метод решения которого (метод интервалов) нам уже известен. Итак, рассмотрим рациональное неравенство
где 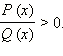 (Такой вид неравенства называется стандартным.) Заметим, что:
(Такой вид неравенства называется стандартным.) Заметим, что:
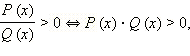 то есть отношение двух многочленов положительно тогда и только тогда, когда положительно их произведение.
то есть отношение двух многочленов положительно тогда и только тогда, когда положительно их произведение.
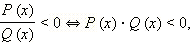 то есть отношение двух многочленов отрицательно тогда и только тогда, когда отрицательно их произведение.
то есть отношение двух многочленов отрицательно тогда и только тогда, когда отрицательно их произведение.
Итак,
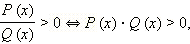 |
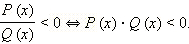 |
Левая часть полученных неравенств есть произведение многочленов, то есть сама является многочленом. А поскольку его знак совпадает со знаком дроби 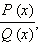 то дробь меняет или не меняет знак при переходе через точку
то дробь меняет или не меняет знак при переходе через точку
Если же двучлен 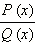 − в степени
− в степени 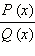 при переходе через точку
при переходе через точку
Таким образом, показан принципиальный метод решения рациональных неравенств. Имея в виду последнее замечание, метод интервалов для рациональных функций можно сформулировать в следующем виде.
Привести неравенство к стандартному виду 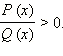
Разложить на множители многочлены
Нули числителя, не совпадающие с нулями знаменателя, отметить на числовой оси точками, а нули знаменателя − кружочками (эти точки, очевидно, не входят в ОДЗ рациональной функции и потому они как будто «выколоты» из числовой оси).
Подставить мысленно в неравенство очень большое число (большее самого большого из корней числителя и знаменателя) для того, чтобы определить, какой знак имеет рациональная функция на самом правом интервале. Провести кривую знаков, проходя через все точки, отмеченные на числовой прямой, меняя или не меняя знак в зависимости от суммарной степени двучлена, отвечающего данной точке.
Записать ответ, обращая особое внимание на граничные точки, часть из которых может быть «выколота».
Таким образом, для нестрогих рациональных неравенств имеем по определению
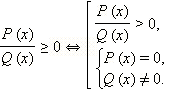 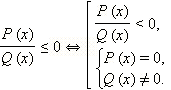 |
Заметим, что на двучлен
 |
 |
 |

