Глава 4. Комбинаторика
4.1.
4.1.1.
Понятие множества − одно из первичных в математике. Поэтому очень трудно дать ему какое-либо определение, которое бы не заменяло слово «множество» каким-нибудь равнозначным выражением, например, совокупность, собрание элементов и т. д. Элементы множества − это то, из чего это множество состоит, например, каждый ученик вашего класса есть элемент множества школьников. Множества обычно обозначают большими буквами: A, B, C, N, ..., а элементы этих множеств − аналогичными маленькими буквами: a, b, c, n, ... Существуют стандартные обозначения для некоторых множеств. Например,
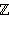 − множество целых чисел;
− множество целых чисел;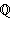 − множество рациональных чисел;
− множество рациональных чисел;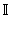 − множество иррациональных чисел;
− множество иррациональных чисел;  − множество действительных чисел;
− множество действительных чисел;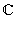 − множество комплексных чисел.
− множество комплексных чисел.
Если элемент a принадлежит множеству A, то пишут: a  A.
A.
Множество считается заданным, если для любого объекта можно определить, принадлежит ли этот объект множеству или нет.
Например, множество всех натуральных чисел 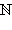 является подмножеством всех действительных чисел
является подмножеством всех действительных чисел  Из определения непосредственно следует, что A
Из определения непосредственно следует, что A  A, то есть всякое множество является подмножеством самого себя.
A, то есть всякое множество является подмножеством самого себя.
В математике часто приходится иметь дело с числовыми множествами. Приведём определения и обозначения множеств, которые имеют общее название числовых промежутков.
| Название промежутка |
Определение |
Обозначение |
| Отрезок от a до b (замкнутое множество) |
a ≤ x ≤ b |
[a; b] |
| Интервал от a до b (открытое множество) |
a < x < b |
(a; b) |
| Открытый слева промежуток от a до b |
a < x ≤ b |
(a; b] |
| Открытый справа промежуток от a до b |
a ≤ x < b |
[a; b) |
| Закрытый числовой луч от a до +∞ |
x ≥ a |
[a; +∞) |
| Открытый числовой луч от a до +∞ |
x > a |
(a; +∞) |
| Закрытый числовой луч от −∞ до a |
x ≤ a |
(−∞; a] |
| Открытый числовой луч от −∞ до a |
x < a |
(−∞; a) |
| Числовая прямая |
−∞ < x < +∞ |
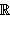 |
|
| Таблица 4.1.1.1 |
Пример 1Задайте перечислением множество B = {x: x2 − 2x + 1 = 0}. Это стандартная запись для задания множества, читается она так: множество элементов x таких, что x2 − 2x + 1 = 0.
Так как уравнение x2 − 2x + 1 = 0 имеет единственный корень x = 1, то множество B состоит из одного элемента B = {1}.
Ответ. B = {1}.
|
Пример 2Определите множество A натуральных чисел, меньших 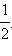
Так как любое натуральное число больше 1 и тем более  то натуральных чисел, обладающих указанным свойством, не
существует, и A = то натуральных чисел, обладающих указанным свойством, не
существует, и A = 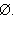
Ответ. A = 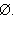
|






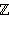 − множество целых чисел;
− множество целых чисел;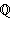 − множество рациональных чисел;
− множество рациональных чисел;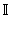 − множество иррациональных чисел;
− множество иррациональных чисел;  − множество действительных чисел;
− множество действительных чисел;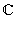 − множество комплексных чисел.
− множество комплексных чисел.








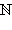 является подмножеством всех действительных чисел
является подмножеством всех действительных чисел  Из определения непосредственно следует, что
Из определения непосредственно следует, что ![]() A
A







