Задачи
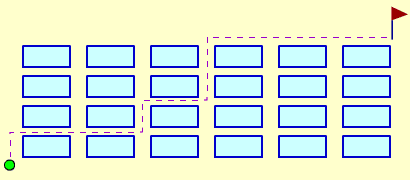
Город имеет вид прямоугольника, разбитого n – 1 улицами, идущими слева направо, и k – 1 перпендикулярными им улицами на n × k кварталов. Сколькими способами человек, идущий из одного угла города, может кратчайшим путем добраться до противоположного ему угла? Решите задачу для n = 6, k = 4.
Решение.
На каждом перекрестке путник совершает выбор: идти налево или прямо. Путник пройдёт через n + k перекрёстков, при этом повернуть или продолжать идти налево он должен на k перекрёстках. Отсюда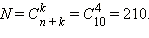 
Ответ: Человек может добраться 210 способами.
4 из 8
 |
