Страховщик обслуживает 500 клиентов, выплачивая каждому из них при наступлении несчастного случая 1000 рублей. В среднем, в год наступает 5 страховых случаев. Какую сумму нужно брать страховщику с каждого клиента, чтобы с вероятностью 98 % иметь по итогам года неотрицательный баланс?
Решение.
Так как клиентов очень много, то задача описывается распределением Пуассона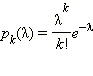 
с параметром λ = 5, где k – количество страховых случаев в год. Составим таблицу:
| k |
pk (5) |
p0 (5) + … +
pk (5) |
| 0 |
0,006738 |
0,006738 |
| 1 |
0,033690 |
0,040428 |
| 2 |
0,084224 |
0,124652 |
| 3 |
0,140374 |
0,265026 |
| 4 |
0,175467 |
0,440493 |
| 5 |
0,175467 |
0,615961 |
| 6 |
0,146223 |
0,762183 |
| 7 |
0,104445 |
0,866628 |
| 8 |
0,065278 |
0,931906 |
| 9 |
0,036266 |
0,968172 |
| 10 |
0,018133 |
0,986305 |
В последней колонке записана вероятность того, что в год произойдёт не больше k страховых случаев. Мы видим, что при k = 10 эта вероятность превысила 98 %.
Таким образом, страховщику нужно рассчитывать на то, что придётся заплатить 10 клиентам по 1000 рублей. Всего у него 500 клиентов – с каждого нужно собрать по 20 рублей.
Отметим, что, в среднем, в год наступает 5 страховых случаев. Это означает, что страховщику придётся выплатить всего 5000 рублей; оставшиеся 5000 рублей он, скорее всего, получит в виде прибыли.
Задачи
5 из 5
