Глава M. Методика

M.3.

M.3.8.

Тема. Показательные и логарифмические неравенства.

Основные понятия. Определение показательного неравенства, определение логарифмического неравенства, теорема о решении показательного неравенства, теорема о решении логарифмического неравенства.

Самостоятельная деятельность учащихся. Решение задач по теме «Показательные и логарифмические неравенства».

Использование новых информационных технологий. В качестве дополнительного иллюстративного материала показ на компьютере модели курса «Показательные и логарифмические неравенства» (используются компьютерные модели 3.2. Решение логарифмических неравенств и 3.3. Решение показательных уравнений).

План урока

Основное содержание урока

Мы считаем целесообразным поработать с моделями 3.2 и 3.3.

В модели 3.2. Решение логарифмических неравенств вы найдёте:

1. примеры графического решения логарифмических неравенств;
2. теоремы для решения логарифмических неравенств; применение этих теорем для решения логарифмических неравенств.

В модели 3.3. Решение показательных уравнений вы найдете:

1. примеры графического решения показательных неравенств;
2. теоремы для решения показательных неравенств; применение этих теорем для решения показательных неравенств.

Мы рекомендуем рассмотреть решение примеров, данных в моделях 3.2 и 3.3, и разобрать их с учащимися.

На обобщающем уроке полезно вспомнить с учащимися:

• определение показательного неравенства;
• определение логарифмического неравенства;
• теорему о решении показательного неравенства;
• теорему о решении логарифмического неравенства.

	Показательными неравенствами называют неравенства вида af (x) > ag (x).

Показательное неравенство af (x) > ag (x) равносильно неравенству того же смысла f (x) > g (x), если a > 1; показательное неравенство af (x) > ag (x) равносильно неравенству противоположного смысла f (x) < g (x), если 0 < a < 1.

	Логарифмическими неравенствами называют неравенства вида loga f (x) > loga g (x), где a – положительное число, отличное от 1, и неравенства, сводящиеся к этому виду.

Если f (x) > 0 и g (x) > 0, то: при a > 1 логарифмическое неравенство loga f (x) > loga g (x) равносильно неравенству того же смысла f (x) > g (x); при 0 < a < 1 логарифмическое неравенство loga f (x) > loga g (x) равносильно неравенству противоположного смысла f (x) < g (x).

Далее мы приводим систему упражнений, с помощью которой можно повторить весь изученный материал по теме «Показательные и логарифмические неравенства» и подготовить учащихся к контрольной работе.

Решите неравенство:

1. 7^2x – 9 > 7^3x – 6;
2. 4^5x – 1 > 16^3x + 2;
3. 23x + 6 ≤
4. 
5. 0,3^6x – 1 – 0,3^6x ≥ 0,7;
6. 5^2x + 4 · 5^x – 5 ≥ 0;
7. 3^2x + 1 – 10 · 3^x + 3 < 0;
8. 3^x < 5^x;
9. 2^2 – x > 2x – 3;
10. 
11. (x – 6)(5^x – 6 – 25) < 0;
12. log₅ (3x + 1) < 2;
13. log₂ (5x – 9) ≤ log₂ (3x + 1);
14. log₈ (x² – 7x) > 1;
15. log_2² x > 4log₂ x – 3;
16. log₃ x > log₃ 72 – log₃ 8;
17. log_5x – 1 2 ≤ 0.
18. Сколько целочисленных решений имеет неравенство
    log₁₂ (x²  – x) ≤ 1?
19. Решите систему неравенств:
20. Решите систему неравенств:

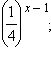
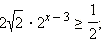
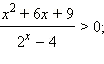
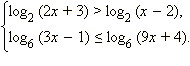
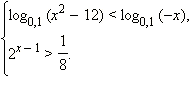
Ответы на вопросы

1. Дайте определение показательного неравенства.
2. Дайте определение логарифмического неравенства.
3. Сформулируйте теорему о решении показательного неравенства.
4. Сформулируйте теорему о решении логарифмического неравенства.

Домашнее задание

№ 1400–1406; № 1582–1586 из задачника А. Г. Мордковича и др. «Алгебра и начала анализа, 10–11 классы».