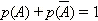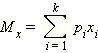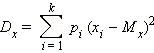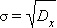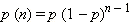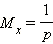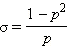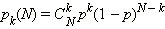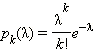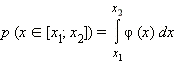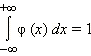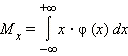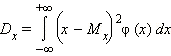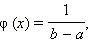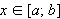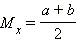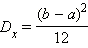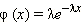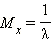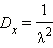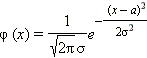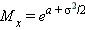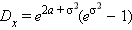Справочник
R.1.
R.1.14. Свойства вероятностей
Нормировка вероятности:
| 0 ≤ p (A) ≤ 1 для любого события A |
Вероятность противоположного события:
Для независимых событий A и B:
| p (A или B) = p (A) + p (B) |
Условная вероятность:
| p (AB) = p (B) · p (A | B) |
Формула полной вероятности:
| p (B) = p (B | A1) p (A1) + p (B | A2) p (A2) + p (B | A3) p (A3) +… + p (B | Ak) p (Ak) |
Дискретные распределения
Математическое ожидание случайной величины, которая может принимать значения x1, x2, ..., xk с вероятностями p1, p2, ..., pk:
Дисперсия такой величины:
Среднеквадратичное отклонение:
Геометрическое распределение:
Биномиальное распределение:
Распределение Пуассона:
Непрерывные распределения
Плотность вероятности:
Вероятность попадания случайной величины в промежуток [x1; x2]:
Нормировка плотности вероятности:
Математическое ожидание:
Дисперсия:
Постоянное распределение:
Показательное распределение:
Нормальное распределение:
Логарифмически-нормальное распределение: