Глава 4. Комбинаторика

Модель 4.4.
Пусть задано некоторое конечное множество из n элементов. Пусть из числа его элементов выбраны k различных штук (k ≤ n), тогда говорят, что произведена выборка объёма k. Если важен порядок, в котором произведена выборка элементов, то говорят об упорядоченной выборке, если порядок не важен, то о неупорядоченной. Неупорядоченная выборка объёма k из множества, состоящего из n элементов (k ≤ n), называется сочетанием из k элементов по n. Упорядоченная выборка называется размещением из k элементов по n.
Выборку элементов удобно иллюстрировать при помощи пронумерованных шаров, находящихся в урне. Таким образом, из урны, в которой изначально содержатся n шаров, каким-либо образом изымаются k шаров. В том случае, если после изъятия из урны очередной шар возвращается в неё, он может быть вытащен повторно. Тогда говорят о сочетании с повторением. Если же шар в урну не возвращается, то говорят о сочетании без повторения.
Для сочетания без повторения 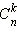 справедлива формула
справедлива формула 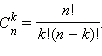 Действительно, из любого набора, содержащего k элементов, можно получить
Действительно, из любого набора, содержащего k элементов, можно получить 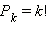 перестановок. Упорядоченных выборок объёма k существует
перестановок. Упорядоченных выборок объёма k существует 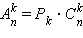 штук. Отсюда и следует справедливость приведённой формулы. Коэффициенты
штук. Отсюда и следует справедливость приведённой формулы. Коэффициенты 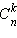 называются биномиальными. Часто вместо
называются биномиальными. Часто вместо 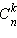 можно встретить обозначение
можно встретить обозначение 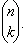
Число сочетаний с повторением 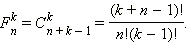 В интерактивном режиме вы можете ввести значения чисел n и k, а также способ выборки. Программа автоматически вычислит число сочетаний соответствующего типа. Нажмите кнопку , чтобы начать анимацию, – чтобы приостановить её и – чтобы вернуть анимацию в исходное состояние.
В интерактивном режиме вы можете ввести значения чисел n и k, а также способ выборки. Программа автоматически вычислит число сочетаний соответствующего типа. Нажмите кнопку , чтобы начать анимацию, – чтобы приостановить её и – чтобы вернуть анимацию в исходное состояние.



 Модель 4.4.
Модель 4.4.
 Модель 4.4.
Модель 4.4.

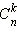 справедлива формула
справедлива формула 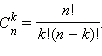 Действительно, из любого набора, содержащего
Действительно, из любого набора, содержащего 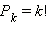 перестановок. Упорядоченных выборок объёма
перестановок. Упорядоченных выборок объёма 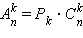 штук. Отсюда и следует справедливость приведённой формулы. Коэффициенты
штук. Отсюда и следует справедливость приведённой формулы. Коэффициенты 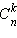 называются биномиальными. Часто вместо
называются биномиальными. Часто вместо 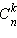 можно встретить обозначение
можно встретить обозначение 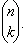
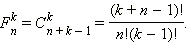 В интерактивном режиме вы можете ввести значения чисел
В интерактивном режиме вы можете ввести значения чисел 

