 Модель 1.14.
Модель 1.14.
 Модель 1.14.
Модель 1.14.
 |
Комплексным числом называется выражение вида 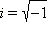 .
.
Комплексные числа часто обозначают одной буквой, например,
Геометрической интерпретацией действительных чисел является координатная прямая. Кроме того, как было установлено выше, на координатной прямой «нет места для новых точек», то есть любой точке на координатной оси отвечает действительное число. Следовательно, комплексные числа на этой прямой расположить уже нельзя, однако можно попытаться рассмотреть наряду с действительной осью, на которой мы будем откладывать действительную часть комплексного числа, ещё одну ось, ей перпендикулярную, и назвать её мнимой осью. Тогда любому комплексному числу
Важной является интерпретация комплексного числа
Модулем комплексного числа называется длина вектора, соответствующего этому числу. Модуль комплексного числа
Пусть
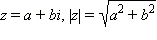 и
и
Такая форма записи комплексного числа называется тригонометрической формой записи комплексного числа. Для того, чтобы перейти от алгебраической формы записи комплексного числа к тригонометрической форме, нужно найти его модуль и один из аргументов.
Также используется показательная форма записи комплексного числа:
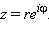
При этом считается, что 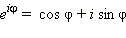 .
.
В интерактивном режиме вы можете ввести комплексное число в алгебраической или тригонометрической форме. Воспользуйтесь кнопками переключения между этими формами. В главном окне модели появится геометрическая интерпретация числа, а в окне вывода – все три формы его записи, а также значения модуля и аргумента комплексного числа. Чтобы перейти в демонстрационный режим, щёлкните по кнопке с кинопроектором. Нажмите кнопку , чтобы начать анимацию, – чтобы приостановить её и – чтобы вернуть анимацию в исходное состояние. Для возвращения в интерактивный режим нажмите на кнопку с изображением руки.


