 Модель 1.15.
Модель 1.15.
 Модель 1.15.
Модель 1.15.
 |
По определению, суммой двух комплексных чисел
Если комплексные числа 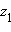 и
и 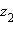 представлены на плоскости векторами
представлены на плоскости векторами
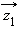 и
и
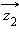 соответственно, то вектор суммы
соответственно, то вектор суммы
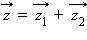 получается из векторов
получается из векторов
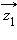 и
и 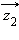 по правилу параллелограмма, а вектор разности
по правилу параллелограмма, а вектор разности
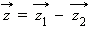 – из векторов
– из векторов
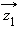 и
и 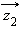 по правилу треугольника.
по правилу треугольника.
Для операции сложения комплексных чисел верны коммутативный и ассоциативный законы:
В интерактивном режиме вы можете ввести комплексное число в алгебраической форме. В главном окне модели появится геометрическая интерпретация суммы или разности введённых чисел (в зависимости от выбранного переключателя из группы ), а в окне вывода – сумма и разность чисел в алгебраической и тригонометрической форме. Чтобы перейти в демонстрационный режим, щёлкните по кнопке с кинопроектором. Нажмите кнопку , чтобы начать анимацию, – чтобы приостановить её и – чтобы вернуть анимацию в исходное состояние. Для возвращения в интерактивный режим нажмите на кнопку с изображением руки.


