 Модель 1.16.
Модель 1.16.
 Модель 1.16.
Модель 1.16.
 |
По определению, произведением двух комплексных чисел
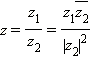 , где
, где
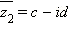 – комплексно сопряжённое для
– комплексно сопряжённое для
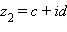 число. Несложно подсчитать, что
число. Несложно подсчитать, что
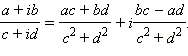
Операции умножения и деления комплексных чисел достаточно просто записываются в тригонометрической форме. Если
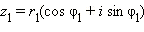 и
и 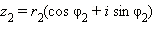 , то
, то
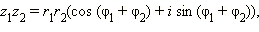
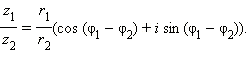
Для операции умножения комплексных чисел верны коммутативный, ассоциативный и дистрибутивный законы:
В интерактивном режиме вы можете вводить комплексные числа в алгебраической или тригонометрической форме. В главном окне модели появится геометрическая интерпретация произведения или частного чисел (в зависимости от выбранного переключателя из группы ), а в окне вывода – произведение и частное чисел в алгебраической и тригонометрической форме. Чтобы перейти в демонстрационный режим, щёлкните по кнопке с кинопроектором. Нажмите кнопку , чтобы начать анимацию, – чтобы приостановить её и – чтобы вернуть анимацию в исходное состояние. Для возвращения в интерактивный режим нажмите на кнопку с изображением руки.


