Глава 4. Комбинаторика

Модель 4.2.
Пусть задано некоторое конечное множество из n элементов. Пусть из числа его элементов выбраны k различных штук (k ≤ n), тогда говорят, что произведена выборка объёма k. Если важен порядок, в котором произведена выборка элементов, то говорят об упорядоченной выборке, если порядок не важен, то о неупорядоченной. Упорядоченная выборка объёма k из множества, состоящего из n элементов (k ≤ n), называется размещением из k элементов по n. Неупорядоченная выборка называется сочетанием из k элементов по n.
Выборку элементов удобно иллюстрировать при помощи пронумерованных шаров, находящихся в урне. Таким образом, из урны, в которой изначально содержатся n шаров, каким-либо образом изымаются k шаров. В том случае, если после изъятия из урны очередной шар возвращается в неё, он может быть вытащен повторно. Тогда говорят о размещении с повторением. Если же шар в урну не возвращается, то говорят о размещении без повторения.
Для размещения без повторения 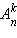 справедлива формула
справедлива формула 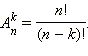 Частным случаем размещения без повторения является перестановка объектов:
Частным случаем размещения без повторения является перестановка объектов: 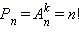 (вспомним, что 0! = 1). Доказательство этой формулы следует из того, что первый элемент можно выбрать n различными способами, второй – (n – 1) способом, третий – (n – 2) способами, k-й – (n – (k – 1)) способом, а последний (n-й) – всего n – (n – 1) = 1 способом. Произведение этих чисел и составляет факториал числа n.
(вспомним, что 0! = 1). Доказательство этой формулы следует из того, что первый элемент можно выбрать n различными способами, второй – (n – 1) способом, третий – (n – 2) способами, k-й – (n – (k – 1)) способом, а последний (n-й) – всего n – (n – 1) = 1 способом. Произведение этих чисел и составляет факториал числа n.
В интерактивном режиме вы можете ввести количество элементов n. Программа автоматически вычислит число перестановок соответствующего типа. Нажмите кнопку , чтобы начать анимацию, – чтобы приостановить её и – чтобы вернуть анимацию в исходное состояние.



 Модель 4.2.
Модель 4.2.
 Модель 4.2.
Модель 4.2.

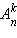 справедлива формула
справедлива формула 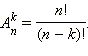 Частным случаем размещения без повторения является перестановка объектов:
Частным случаем размещения без повторения является перестановка объектов: 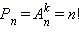 (вспомним, что 0! = 1). Доказательство этой формулы следует из того, что первый элемент можно выбрать
(вспомним, что 0! = 1). Доказательство этой формулы следует из того, что первый элемент можно выбрать 

