 Модель 4.1.
Модель 4.1.
 Модель 4.1.
Модель 4.1.
 |
Интерактивная модель демонстрирует основы теории множеств на примере множеств на плоскости. Основные операции над множествами:
Понятия множества и подмножества используются при определении многих понятий математики и, в частности, при определении геометрической фигуры. Определим как универсальное множество плоскость. Тогда можно дать следующее определение геометрической фигуры в планиметрии:
Геометрической фигурой называется всякое множество точек плоскости. Чтобы наглядно отображать множества и отношения между ними, рисуют геометрические фигуры, которые находятся между собой в этих отношениях. Такие изображения множеств называют диаграммами Эйлера–Венна. Диаграммы Эйлера–Венна делают наглядными различные утверждения, касающиеся множеств. На них универсальное множество изображают в виде прямоугольника, а его подмножества – кругами.
Тип операции над множествами можно выбрать при помощи группы переключателей. Если вы установите один или оба флажка в выключателях 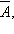
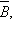 то соответствующий символ во всех формулах заменится его отрицанием. Можно изменять взаимное расположение диаграмм Эйлера–Венна, обозначающих отдельные множества на плоскости; при этом будет меняться результат операции над ними.
то соответствующий символ во всех формулах заменится его отрицанием. Можно изменять взаимное расположение диаграмм Эйлера–Венна, обозначающих отдельные множества на плоскости; при этом будет меняться результат операции над ними.
Переключившись в демонстрационный режим при помощи кнопки с изображением кинопроектора, можно просмотреть анимацию. Кнопка запускает её, кнопка – приостанавливает, а кнопка возвращает анимацию в исходное состояние. Кнопка с изображением руки переводит модель обратно в интерактивный режим.


