Алгебраические операции над функциями Задачи с решениями
Задачи с решениями

Постройте эскиз графика функции
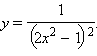
Решение
Построим сначала график знаменателя. y = 2x2 – 1 – это парабола, растянутая от оси абсцисс и сдвинутая на 1 вниз. Она пересекает ось OX в точках
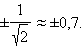 При возведении этой функции в квадрат точки
При возведении этой функции в квадрат точки
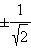 останутся нулями, а все остальные ординаты будут положительными. В точке x = 0 ордината будет равна 1; при движении по числовой оси вправо функция сначала будет убывать до 0, затем, начиная с точки
останутся нулями, а все остальные ординаты будут положительными. В точке x = 0 ордината будет равна 1; при движении по числовой оси вправо функция сначала будет убывать до 0, затем, начиная с точки
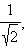 начнет возрастать вверх. Так как функция 2x2 – 1 четная, левая половина графика (вплоть до оси OY) зеркально повторяет правую.
начнет возрастать вверх. Так как функция 2x2 – 1 четная, левая половина графика (вплоть до оси OY) зеркально повторяет правую.
Вернемся к искомой функции. Ее числитель всегда постоянен и равен 1. В точке x = 0 значение этой функции равно 1. На интервале (0; 1) знаменатель убывает до нуля; значит, функция возрастает до бесконечности. Прямая x = 1 – вертикальная асимптота. Далее знаменатель возрастает; сама же функция убывает из бесконечности при x = 1, асимптотически стремясь к нулю при x → ∞. В левой части графика картина та же самая: функция
 как и ее знаменатель, является четной.
как и ее знаменатель, является четной.
 4 из 4
4 из 4
 |


 Задачи с решениями
Задачи с решениями

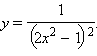
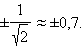
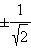
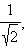

 4 из 4
4 из 4
