Диаметр окружности с центром в начале координат лежит на касательной к параболе y = x2 + x + 1. Найдите радиус этой окружности, если она проходит через точку касания. Точка касания находится слева от оси ординат.
Решение.
Производная функции y равняется
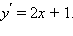Уравнение касательной к параболе
Т.к. касательная проходит через начало координат, то она является графиком прямой пропорциональности и
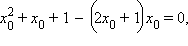
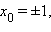
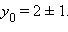
Т.к. точка касания находится слева, то ее координаты равны A (–1; 1). Точка A принадлежит не только параболе, но и окружности. Отсюда
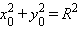
и
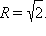
function showUserAnswer(){
testSolution='
Задачи
7 из 7
