Глава 3. Дифференцирование и интегрирование функций
3.2. Исследование функций при помощи производных
3.2.3. Выпуклость функции и точки перегиба
Непрерывная на отрезке [a; b] функция f (x) называется выпуклой вверх на этом отрезке, если для любых точек x1 и x2 из этого отрезка
|
|
| График 3.2.3.1. Выпуклая вверх функция
|
Другими словами, если для любых точек x1 и x2 отрезка [a; b] секущая AB проходит под графиком функции f (x), то функция f выпукла вверх.
Аналогично определяется функция, выпуклая вниз.
Дважды дифференцируемая на [a; b] функция f (x) выпукла вверх, если для любого
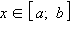
Дважды дифференцируемая на [a; b] функция f (x) выпукла вниз, если для любого
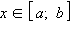
Так, вторая производная функции 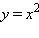 равна
равна
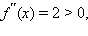 откуда следует, что квадратичная функция выпукла вниз на всей области определения.
откуда следует, что квадратичная функция выпукла вниз на всей области определения.
Пусть функция f (x) непрерывна в точке 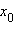 и имеет в этой точке конечную или бесконечную производную. Тогда точка
и имеет в этой точке конечную или бесконечную производную. Тогда точка 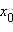 называется точкой перегиба функции f, если в этой точке изменяется направление ее выпуклости.
называется точкой перегиба функции f, если в этой точке изменяется направление ее выпуклости.
Необходимое условие наличия точки перегиба. Если 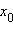 – точка перегиба функции f (x), и функция f (x) имеет вторую производную, непрерывную в этой точке, то
– точка перегиба функции f (x), и функция f (x) имеет вторую производную, непрерывную в этой точке, то
Достаточные условия наличия точки перегиба.
Пусть функция f (x) непрерывна и имеет конечную или бесконечную производную в точке 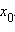 Если
Если
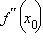 меняет знак при переходе через точку
меняет знак при переходе через точку 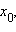 то
то 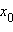 – точка перегиба функции f (x).
– точка перегиба функции f (x).
Если
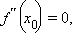
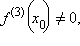 то
то 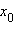 – точка перегиба функции f (x).
– точка перегиба функции f (x).
В заключение приведем примеры, когда точка x0 не является точкой перегиба несмотря на то, что ее вторая производная меняет знак при переходе через эту точку:
-
если функция разрывна в точке
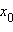 (например
(например 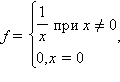
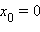 );
);
-
в случае угловой точки (например,
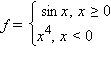
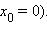
Не являются точками перегиба и точки возврата, например точка 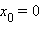 у функции
у функции 
Все вышеперечисленные случаи изображены на рисунке.
|
|
| График 3.2.3.2. Точки, не являющиеся точками перегиба: точка разрыва, точка возврата, угловая точка |







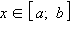

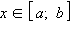
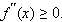
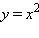 равна
равна
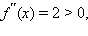
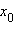 и имеет в этой точке конечную или бесконечную производную. Тогда точка
и имеет в этой точке конечную или бесконечную производную. Тогда точка 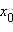 называется точкой перегиба функции
называется точкой перегиба функции 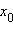 – точка перегиба функции
– точка перегиба функции 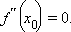
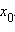 Если
Если
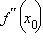
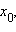 то
то 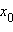 – точка перегиба функции
– точка перегиба функции 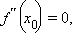
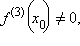
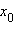 – точка перегиба функции
– точка перегиба функции 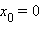 у функции
у функции 




