Глава 3. Дифференцирование и интегрирование функций
3.4. Определенный интеграл
3.4.5. Определенные интегралы в физике
Мы уже упоминали, что интегральное исчисление применяется для нахождения пути, пройденного материальной точкой, по закону изменения его скорости. Какие еще задачи решают при помощи понятия интеграла в физике?

 |
|
Модель 3.14.
Движение с переменным ускорением
|
1. Пусть материальная точка движется с ускорением a (t). Тогда ее скорость равна
а перемещение –
где v0, x0 – постоянные, определяемые из начальных условий, t0 и t – начальный и конечный моменты времени.
2.
 1
|
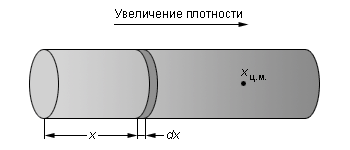
| Рисунок 3.4.5.1. Центр масс
|
Пусть плотность ρ (x) стержня с постоянным сечением S зависит от расстояния до начала стержня. Тогда масса стержня равна
где L – длина стержня, а центр масс стержня находится на расстоянии
3. Работа газа при его расширении от объема V1 до объема V2 равна
где P (V) – давление газа в этом процессе.

 |
|
Модель 3.15.
Работа газа
|




















