Глава 2. Элементарные функции и их графики

Модель 2.10.  Математический маятник

Зависимость координаты конца математического маятника от времени определяется тригонометрической функцией – синусом или косинусом: 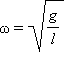x (t) = x₀ cos ωt, где угловая частота ω определяется длиной маятника: .

Задайте при помощи полей численного ввода длину маятника l и начальное отклонение x₀. Нажмите кнопку Старт. Маятник начнет колебаться, выписывая кривую на движущемся полотне. Эта же кривая отображается на графике в нижней части модели.

Кнопка Стоп приостанавливает анимацию, кнопка Сброс возвращает модель в исходное состояние.