Глава 1. Механика Задачи с решениями
Задачи с решениями

Два упругих шарика подвешены на тонких нитях так, что они находятся на одной высоте и соприкасаются. Нити подвеса имеют разные длины: l1 = 0,9 м и l2 = 0,4 м. Массы шариков m1 = 80 г и m2 = 160 г соответственно. Шарик с массой m1 отклоняют на угол φ = 60° и отпускают. Считая удар абсолютно упругим, определите, на какой угол отклонится второй шарик после удара.
РешениеСкорость u шарика m1 перед ударом находится из закона сохранения механической энергии:
u2 = 2gh1 = 2gl1(1 – cos φ) = gl1.
Здесь h1 = l1(1 – cos φ) – начальная высота подъема первого шарика, φ = 60° – угол отклонения.
В момент удара внешние силы в горизонтальном направлении на шарики не действуют, поэтому справедлив закон сохранения количества движения:
m1u = m1υ1 + m2υ2,
где υ1 и υ1 – скорости шариков после удара. При абсолютно упругом ударе выполняется закон сохранения механической энергии:
Из этих соотношений получим:
После удара первый шарик отскочит назад (так как m1 < m2) и поднимется на высоту 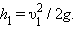 Второй шарик поднимется на высоту (рис. 1.21.2)
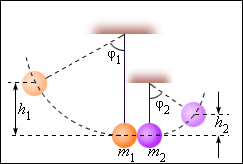
Второй шарик поднимется на высоту (рис. 1.21.2)
|
| Рисунок 1.21.2.
|
Угол отклонения φ2 второго шарика находится из условия
Следовательно, φ2 = 60°.
 2 из 2
2 из 2
 |


 Задачи с решениями
Задачи с решениями

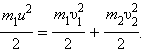
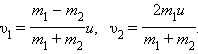
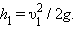 Второй шарик поднимется на высоту (рис. 1.21.2)
Второй шарик поднимется на высоту (рис. 1.21.2)


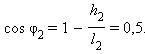
 2 из 2
2 из 2
